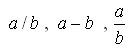عدد کسری
فهرست علوم
فهرست مباحث ریاضیات
چند جلسه مربوط به مرور اجمالی تاریخ و مباحث ریاضیات
جایگاه ریاضیات در نظام آموزشی حوزه های علمیه
علم حساب
قضیه اساسی حساب
عدد گنگ-العدد الاصم
عدد گویا یا عدد کسری (به انگلیسی: Rational number) در علم ریاضیات، عددی است که میتواند به صورت کسر p q  (یا p / q
(یا p / q  ) از دو عدد صحیح p
) از دو عدد صحیح p  و q
و q  ( به طوری که p
( به طوری که p  صورت کسر و q
صورت کسر و q  مخرج کسر باشد.) بیان شود.[۱] به عبارت دیگر، اعداد گویا کسرهایی هستند که از تقسیم عدد صحیح بر عدد صحیح دیگر (به جز صفر) پدید آمده باشد.[۲] از آنجایی که q
مخرج کسر باشد.) بیان شود.[۱] به عبارت دیگر، اعداد گویا کسرهایی هستند که از تقسیم عدد صحیح بر عدد صحیح دیگر (به جز صفر) پدید آمده باشد.[۲] از آنجایی که q  میتواند برابر با عدد یک باشد؛ پس تمامی اعداد صحیح، طبیعی و حسابی، عدد گویا نیز هستند.
میتواند برابر با عدد یک باشد؛ پس تمامی اعداد صحیح، طبیعی و حسابی، عدد گویا نیز هستند.
نماد ریاضی اعداد گویا
مجموعه اعداد گویا معمولاً با حرف Q  نمایش داده میشوند که به انتخابِ جوزپه پئانو از ابتدای کلمهٔ ایتالیاییِ quoziente، بهمعنای خارجقسمت، اخذ شدهاست.[۳]
نمایش داده میشوند که به انتخابِ جوزپه پئانو از ابتدای کلمهٔ ایتالیاییِ quoziente، بهمعنای خارجقسمت، اخذ شدهاست.[۳]
تعریف
بهطور کلی میتوان مجموعه اعداد گویا را بدین صورت تعریف کرد: اگر ما یک عدد طبیعی داشته باشیم و آن را (مثلا x  ) بر دیگری (مثلا y
) بر دیگری (مثلا y  ) تقسیم کنیم؛ به طوری که (یا به شرطی که) هم x
) تقسیم کنیم؛ به طوری که (یا به شرطی که) هم x  (صورت) و هم y
(صورت) و هم y  (مخرج) عضو مجموعه اعداد صحیح ( Z
(مخرج) عضو مجموعه اعداد صحیح ( Z  ) باشند؛ و y
) باشند؛ و y  (مخرج) برابر با صفر نباشد؛ آنگاه نسبت x
(مخرج) برابر با صفر نباشد؛ آنگاه نسبت x  به y
به y  (کسر مورد نظر) عددی گویا خواهد بود. [۴] Q = { x y ∣ x , y ∈ Z , y ≠ 0 }
(کسر مورد نظر) عددی گویا خواهد بود. [۴] Q = { x y ∣ x , y ∈ Z , y ≠ 0 } 
نکات مهم
- اجتماع مجموعه اعداد گویا Q
 و اعداد گنگ Q c
و اعداد گنگ Q c  (یعنی متمم اعداد گویا) برابر با مجموعه اعداد حقیقی است؛ و همچنین اشتراک این دو مجموعه برابر با ∅
(یعنی متمم اعداد گویا) برابر با مجموعه اعداد حقیقی است؛ و همچنین اشتراک این دو مجموعه برابر با ∅  (تهی) میباشد :
(تهی) میباشد :
Q ∪ Q c = R 
Q ∩ Q c = ∅ 
- نسبت 3 2
 با اینکه یک کسر است؛ اما یکی از شروط اعداد گویا این است که صورت و مخرج، عددی صحیح باشند؛ در صورتی که صورت یا مخرج، عددی رادیکالی باشد و جذر آن کامل نباشد؛ حاصل رادیکال عددی گنگ خواهد بود. پس این کسر، یک عدد گنگ است. اما نسبت 4 2
با اینکه یک کسر است؛ اما یکی از شروط اعداد گویا این است که صورت و مخرج، عددی صحیح باشند؛ در صورتی که صورت یا مخرج، عددی رادیکالی باشد و جذر آن کامل نباشد؛ حاصل رادیکال عددی گنگ خواهد بود. پس این کسر، یک عدد گنگ است. اما نسبت 4 2  یک عدد گویا میباشد؛ زیرا حاصل صورت این کسر جذر کامل میباشد.
یک عدد گویا میباشد؛ زیرا حاصل صورت این کسر جذر کامل میباشد.
- اعداد صحیح، طبیعی و حسابی ، زیر مجموعهای از اعداد گویا هستند. زیرا مخرج تمامی آنها برابر با یک است. (به عبارت سادهتر همانطور که میدانیم مخرج ۱ هیچ تاثیری در ماهیت عدد ندارد؛ یعنی اگر ما یک عدد دلخواه مانند x
 را داشته باشیم و به مخرج آن ۱ بدهیم؛ کسر با صورت x
را داشته باشیم و به مخرج آن ۱ بدهیم؛ کسر با صورت x  و مخرج ۱، هیچ تفاوتی با خود عدد x
و مخرج ۱، هیچ تفاوتی با خود عدد x  نخواهد داشت. که به صورت ریاضی x 1 = x
نخواهد داشت. که به صورت ریاضی x 1 = x  میشود.) بنابراین میتوانیم با دادن عدد یک به مخرج هر یک از آنها کسری داشته باشیم که تمامی شرایط یک عدد گویا را دارد؛
میشود.) بنابراین میتوانیم با دادن عدد یک به مخرج هر یک از آنها کسری داشته باشیم که تمامی شرایط یک عدد گویا را دارد؛
- اعداد اعشاری را میتوان جزو اعداد گویا به حساب آورد؛ زیرا هر عدد اعشاری را میتوان به صورت کسری نوشت که مخرج آن یکی از توانهای مثبت ۱۰ و صورت آن یک عدد صحیح باشد. برای نمایش آنان روی محور میتوان آنان را به کسر تبدیل نمود :
x 10 n ∈ Q  ⇒
⇒  x ∈ Z
x ∈ Z  , n ∈ N
, n ∈ N 
- بین دو عدد گویا بینهایت عدد گویا وجود دارد. اعداد گویا از منفی بینهایت تا مثبت بینهایت ادامه دارند.
- بین دو عدد گنگ بی شمار عدد گنگ وجود دارد.
مقایسه
برای مقایسه اعداد گویای مثبت، پس از هم مخرج کردن، صورتهایشان مورد مقایسه قرار میگیرد؛ صورت هر کدام که بزرگتر بود، آن عدد بزرگتر است. برای هم مخرج کردن، صورت و مخرج هر یک از اعداد گویا در مخرج دیگری ضرب میشود.
- نکته: بین دو عدد گویای مثبت که صورتشان برابر است، عددی که مخرجش کوچکتر باشد، از عدد دیگر بزرگتر است.
برای مقایسه دو عدد گویای a b  و c d
و c d  بهصورت زیر مخرجها یکی میشوند:
بهصورت زیر مخرجها یکی میشوند:
a b = a × d b × d , c d = c × b d × b 
سپس صورت دو کسر بهدستآمده مورد مقایسه قرار میگیرند: a × d ? c × b 
مثال
دو عدد 5 11  و 3 7
و 3 7  بهصورت زیر مقایسه میشوند:
بهصورت زیر مقایسه میشوند:
3 7 = 3 × 11 7 × 11 = 33 77 , 5 11 = 5 × 7 11 × 7 = 35 77 ⇒ 33 < 35 ⇒ 3 7 < 5 11 
اعمال اصلی ریاضی
جمع و تفریق
برای جمع و تفریق اعداد گویا ابتدا مخرج کسرها یکسان شده، سپس صورتها با هم جمع یا تفریق میشوند:
a b ± c d = a d ± b c b d 
مثال
4 3 + 2 5 = 20 + 6 15 = 26 15 
5 6 − 5 4 = 20 − 30 24 = − 10 24 
ضرب
برای ضرب اعداد گویا، صورتها را در هم و مخرجها نیز در هم ضرب میشوند.
a b ⋅ c d = a c b d 
مثال
2 5 ⋅ 14 35 = 2 × 14 5 × 35 = 28 175

تقسیم
برای تقسیم دو عدد گویا، عدد اول را در معکوس عدد دوم ضرب میشود.
a b ÷ c d = a b . d c = a d b c 
مثال
5 7 ÷ 3 5 = 5 7 ⋅ 5 3 = 5 × 5 7 × 3 = 25 21 
توزیع پذیری منفی و قرینه کسر
برای توزیع پذیری علامت منفی پشت پرانتز به کسر داخل پرانتز، کافی است؛ که پرانتز را حذف کنیم؛ و صورت یا مخرج کسر را قرینه نماییم.
− ( a b ) = − a b = a − b 
مثال
− ( 7 12 ) = − 7 12 = 7 − 12 
توان منفی کسر
اگر کسری را به توان عددی منفی برسانیم؛ برای اینکه بتوانیم توانی مثبت داشته باشیم؛ فقط کافی است که، کسر مذکور را معکوس نموده و خود توان را قرینه نماییم.
( x y ) − n = ( y x ) n 
مثال
( 3 5 ) − 2 = ( 5 3 ) 2 
توزیع پذیری توان نسبت به صورت و مخرج در کسر
اگر ما کسری داشته داشته باشیم و کل کسر را به توان عددی طبیعی برسانیم؛ برای توزیع پذیری توان به صورت جداگانه نسبت به صورت و مخرج، فقط کافی است؛ که به طور جداگانه هم صورت و هم مخرج کسر را به توان همان عدد برسانیم.
( a b ) n = a n b n 
مثال
( 10 17 ) 3 = 10 3 17 3 
توان صفر
اگر عدد یا کسری به غیر از صفر به توان صفر برسد؛ آنگاه حاصل برابر با ۱ خواهد شد.( 0 ≠ x  )
)
( x y ) 0 = 1 
مثال
( 13 − 5 ) 0 = 1 
کسر (به انگلیسی: Fraction) (از لاتین fractus به معنی "شکسته")، نمایشگر جزئی از یک کل یا بهطور کلی تر، هر تعداد از اجزای مساوی با هم است. هنگام صحبتهای روزمره، کسر را جهت توصیف اینکه چه تعداد از اجزایی با اندازههای مشخص وجود دارند، به کار میبرند، مثل: یک دوم، هشت پنجم، سه چهارم. کسر رایج، متعارف یا ساده (مثالها: 1 2  و 17 3
و 17 3  ) شامل یک صورت (Numerator) است که بالای خط قرار میگیرد (یا قبل از اسلش، مثل: 1⁄2)، و مخرج (Denominator) ناصفری که زیر آن خط قرار داده میشود. صورتها و مخرجها در کسرهایی که رایج نیستند نیز به کار میروند، انواع کسرهای غیر رایج شامل این مواردند: کسر مرکب،کسر نامناسب و اعداد مخلوط.
) شامل یک صورت (Numerator) است که بالای خط قرار میگیرد (یا قبل از اسلش، مثل: 1⁄2)، و مخرج (Denominator) ناصفری که زیر آن خط قرار داده میشود. صورتها و مخرجها در کسرهایی که رایج نیستند نیز به کار میروند، انواع کسرهای غیر رایج شامل این مواردند: کسر مرکب،کسر نامناسب و اعداد مخلوط.
نحوه نمایش کسرها
نمایش کسر به صورت یک خط افقی و یک عدد در بالا و یک عدد در پایین میباشد. عدد بالایی صورت کسر و عدد پایینی مخرج کسر نامیده میشود.
2 4 
در اینجا ۲ صورت کسر و ۴ مخرج کسر میباشد.

در این پویا نمایی برابر کسرهای زیر نشان داده شدهاست . 1 4 = 2 8 = 3 2 = 4 16 
انواع کسر
کسر متعارفی
کسر متعارفی نوعی خاصی از کسر است که بنا بر تعریف، هم صورت و هم مخرج آن اعداد صحیح هستند (مخرج باید مخالف صفر باشد). به عنوان مثال، اعداد 4 3  و 9 6
و 9 6  کسر متعارفی هستند، ولی 4 1.2
کسر متعارفی هستند، ولی 4 1.2  و 5 / 3 / 2 / 1
و 5 / 3 / 2 / 1  کسر متعارفی نمیباشند.
کسر متعارفی نمیباشند.
انواع کسر متعارفی
کسر بزرگتر از واحد و کوچکتر از واحد
کسر متعارفی a b  را در نظر بگیرید. اگر صورت از مخرج کسر بزرگتر باشد، یعنی داشته باشیم a>b، کسر از یک (واحد) بزرگتر است. در این صورت a b
را در نظر بگیرید. اگر صورت از مخرج کسر بزرگتر باشد، یعنی داشته باشیم a>b، کسر از یک (واحد) بزرگتر است. در این صورت a b  را کسر بزرگتر از واحد (Improper Fraction) مینامند. گاهی کسرهای بزرگتر از واحد را به صورت عدد مخلوط نشان میدهند.
را کسر بزرگتر از واحد (Improper Fraction) مینامند. گاهی کسرهای بزرگتر از واحد را به صورت عدد مخلوط نشان میدهند.
برعکس، اگر در کسر a b  صورت از مخرج کوچکتر باشد، یعنی a<b، کسر را کوچکتر از واحد (Proper Fraction) مینامند.
صورت از مخرج کوچکتر باشد، یعنی a<b، کسر را کوچکتر از واحد (Proper Fraction) مینامند.
کسر اعشاری و درصدی
کسر اعشاری، یک کسر متعارفی است که مخرج آن ۱۰ یا توانی از ۱۰ است. اغلب برای نمایش کسرهای اعشاری از علامت ممیز (/) استفاده میشود. برای مثال کسر متعارفی 1 10  را میتوان به صورت ۰/۱ نشان داد. همچنین کسر a b
را میتوان به صورت ۰/۱ نشان داد. همچنین کسر a b  را میتوان با ضرب صورت و مخرج در مقدار ۵ به صورت 60 100
را میتوان با ضرب صورت و مخرج در مقدار ۵ به صورت 60 100  یا ۰/۶۰ و حتی بهطور خلاصهتر ۰/۶ نشان داد. کسرهای اعشاری را با نماد علمی نیز میتوان نشان داد.
یا ۰/۶۰ و حتی بهطور خلاصهتر ۰/۶ نشان داد. کسرهای اعشاری را با نماد علمی نیز میتوان نشان داد.
برای نمایش اعداد اعشاری که دارای بینهایت رقم تکرار شونده اعشار هستند، از کسر متعارفی استفاده میشود. برای مثال کسر متعارفی 1 3  بیانگر مقدار …۰/۳۳۳۳ است.
بیانگر مقدار …۰/۳۳۳۳ است.
اگر مخرج کسر قابل تبدیل به ۱۰۰ باشد میتوان اعداد را به صورت درصدی (Percentage) یا به صورت نماد ٪ نیز نشان داد. برای مثال کسر متعارفی 5 100  همان مقدار ۵٪ یا ۰/۰۵ است و 29 100
همان مقدار ۵٪ یا ۰/۰۵ است و 29 100  مقدار ۲۹٪ را نشان میدهد.
مقدار ۲۹٪ را نشان میدهد.
کسر مولد اعشار مختوم
اگر با تقسیم صورت بر مخرج، به باقیمانده صفر برسیم، کسر را مولد اعشار مختوم مینامند. این حالت در زمانی رخ میدهد که مخرج کسر فقط شامل عاملهای ۲ یا ۵ یا هر دو باشد.
کسر مولد اعشاری متناوب
کسرهای وجود دارند که در آنها حاصل تقسیم صورت بر مخرج، باقیمانده صفر نخواهند داشت. به این ترتیب عدد اعشاری حاصل، مختوم نخواهد بود. برای مثال کسرهایی نظیر 1 3  و 1 11
و 1 11  یک عدد اعشاری با مقدار اعشار متناوب ایجاد میکنند. ارقام تکرار شده در تناوب عدد اعشاری را دوره گردش مینامند. از آنجایی که مخرج این گونه کسرها دارای عاملهای اول به غیر از ۲ و ۵ هستند، تقسیم صورت بر مخرج، باقیمانده صفر نخواهند داشت.
یک عدد اعشاری با مقدار اعشار متناوب ایجاد میکنند. ارقام تکرار شده در تناوب عدد اعشاری را دوره گردش مینامند. از آنجایی که مخرج این گونه کسرها دارای عاملهای اول به غیر از ۲ و ۵ هستند، تقسیم صورت بر مخرج، باقیمانده صفر نخواهند داشت.
2 3 = 0.666...  و 1 11 = 0.090909...
و 1 11 = 0.090909... 
کسر مولد اعشاری متناوب مرکب
در این گونه کسرها، با تجزیه مخرج به عوامل اول به ارقام ۲ یا ۵ و یک یا چند عدد اول دیگر میرسیم. در این صورت عدد اعشاری شامل دو قسمت تکراری با گردش و بدون گردش خواهد بود. برای مثال کسر 8 15  از این گونه کسرها محسوب میشود، زیرا مخرج آن به عاملهای ۵ و ۳ تجزیه میشود.
از این گونه کسرها محسوب میشود، زیرا مخرج آن به عاملهای ۵ و ۳ تجزیه میشود.
8 15 = 0.5333... 
کسرهای مخلوط و متعارف
معمولاً کسرهای متعارفی بزرگتر از ۱ را به صورت اعداد مخلوط نشان میدهند. در این حالت عدد مخلوط شامل یک قسمت عدد صحیح و یک کسر متعارفی کوچکتر از واحد است. قسمت عدد صحیح همان خارج قسمت تقسیم و صورت کسر، باقیمانده تقسیم و مخرج کسر متعارفی نیز مقسومٌ علیه خواهد بود.
36 5 = 7 1 5 
کسر نامتعارف
اگر مخرج کسری صفر باشد، مانند 1 0  آن کسر تعریف نشدهاست.
آن کسر تعریف نشدهاست.
تاریخ پیدایش کسر متعارفی
کسر متعارفی در جریان اندازهگیری و زمانی پدید آمد که ناچار شدند واحد اندازهگیری را بشکنند؛ چرا که برای ادامه اندازهگیری، نتوانستند از واحد استفاده کنند. این موضوع، به ویژه از پیدایش کسرهای مشخص، پیش از پیدایش مفهوم کلی کسر، روشن میشود.
زمان زیادی لازم بود تا «نیم» و «یک چهارم» به صورت ۱/۲ و ۱/۴ برای هر نوع واحدی (طول، حجم، وزن، زمان) به کار رود.
در هزاره دوم پیش از میلاد بود که بشر توانست از کسر، همچون بخشی از واحد، استفاده کند. در بابل کهن، حتی نمادهای خاصی برای برخی کسرهای متعارفی وجود داشت.
گویا صفت فاعلی از مصدر گفتن میباشد و در ریاضی هر شمار کسری مانند یا هر عددی که بتوان آن را به شکل یک کسر نوشت را یک عدد گویا مینامیم. مانند ۲-، ۰، ۳+ ،۲/۳ -، ۲۵/- که به ترتیب به شکل کسرهای میتوان نوشت. بهطور کلی هر عددی که بتوان آن را به صورت کسر نوشت، بهطوریکه صورت و مخرج آن متعلق به اعداد صحیح باشند و مخرج آن مخالف صفر باشد یک عدد گویا میگویند. مجموعه اعداد گویا را با حرف Q حرف اول کلمهٔ Quotient به معنی «خارج قسمت» نمایش میدهند.
ضرب کسر
ضرب کسر دارای انواع مختلفی است از جمله: ضرب عدد در کسر (ضرب کسر در عدد) و ضرب کسر در کسر
ضرب عدد در کسر
ابتدا به عدد مخرج یک میدهیم و سپس صورت در صورت و مخرج در مخرج ضرب میشود. 2 × 9 6 = 2 1 × 9 6 = 18 6 
ضرب کسر در عدد
این مورد دقیقاً شبیه ضرب عدد در کسر میباشد و ابتدا باید به عدد مخرج یک بدهیم و سپس در هم ضرب کنیم. 4 5 × 2 = 4 5 × 2 1 = 8 5 
ضرب کسر در کسر
در این نوع ضرب صورت در صورت و مخرج در مخرج ضرب میشوند. 5 7 × 9 5 = 5 7 × 9 5 = 45 35 
دقت کنید در کسرهای که به صورت عدد مخلوط هستند، ابتدا عدد مخلوط را به کسر تبدیل کنید و سپس ضرب را انجام دهید. 4 2 3 × 1 4 5 = 14 3 × 9 5 = 126 15 
تقسیم کسر
برای تقسیم دو کسر متعارفی میتوان آن را به صورت حاصلضرب نوشت و عملیات را مطابق با عملیات ضرب انجام داد. برای این کار کافی است که کسر مقسوم علیه را به صورت معکوس درآورده و در مقسوم ضرب کنیم.
a b ÷ c d = a b × d c 
جمع و تفریق کسر
جمع و تفریق دو کسر متعارفی با مخرج یکسان
اگر مخرج همه کسرها با هم مشابه است، صورت تمام کسرها را با هم جمع میشوند. مخرج نیز همان مخرج یکسان کسرها میباشد.
1 4 + 2 4 = 3 4 
جمع و تفریق دو کسر متعارفی با مخرج متفاوت
دو مخرج (یا هر چند تا که هست) را در هم ضرب کرده تا مخرج مشترک به دست بیاید. اگر یکی از مخرجها به بقیه مخرجها بخش پذیر بود، کافی است آن مخرج به عنوان مخرج مشترک انتخاب شود. صورتها متناسب با مخرج مشترک، بزرگ میشوند. در این حالت صورت کسرها با هم جمع میشوند.
1 3 + 3 5 = 5 15 + 9 15 = 14 15 
ویسنده: والدک مِین ویل (1)
ترجمه: مهران اخباریفر
کسرها در قدیمی ترین اسناد ریاضی یافته شده وجود دارند. اما ملل باستان، رهیافتی عمومی برای کار با کسرها نداشتند و در نتیجه، روش های خاص کار با کسرها اغلب محدودیتهایی در کاربرد آن ها ایجاد می کرد.
بابلی ها از 2000 سال پیش از میلاد از کسر استفاده می کردند. این کسرها به شکل ارزش مکانی نوشته می شدند و اساساً همانند کسرهای اعشاری امروزین بودند؛ اما مخروج ها، که نوشته نمی شدند، توان های متوالی شصت بودند و جداکننده ای که متناظر با ممیز اعشاری باشد وجود نداشت.
پاپیروس رایند، که گاهی پاپیروس احمس هم نامیده می شود، حاوی اولین برخورد نظام مند با کسرهای واحد است. کسرهایی را که نمی شد فقط با یک کسر واحد نمایش داد، به صورت مجموع دو یا چند کسر واحد نمایش می دادند ولی بین آن ها به جای علامت جمع فقط فاصله می گذاشتند. مثلاً 2/35 به صورت 1/42[+]1/30 نشان داده شده است. کسرهای واحد با یک نماد کسر که مخرج زیر آن قرار گرفته است نمایش داده شده اند. در هیروگلیف (نوشتار تصویری)، 1/4 به صورت ### و 1/13 به صورت ### نوشته می شد. کسر 2/3 با نماد خاص ### و 1/2 گاهی با نماد ### نوشته می شد. در هیراتیکِ شکسته، کسرهای واحد را با یک نقطه یا نماد دیگری به نام رو (2) که روی مخرج می گذاشتند نشان می دادند.
یونانی ها نیز اغلب متکی به کسرهای واحد بودند. آنان برای نمایش کسرهای واحد، اغلب مخرج را با یک یا دو علامت تکیه می نوشتند؛ مثلاً
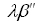
برای 1/32. اما ریاضیدانان یونانی خود را با کسرهای واحد محدود نکردند. گاهی کسرهای کلی را با یک بار نوشتن صورت با یک علامت تکیه و دوبار نوشتن مخرج با دو علامت تکیه نمایش می دادند؛ مثلاً،
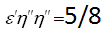
. در بعضی موارد، مخرج را جای می نوشتند که ما امروزه نما را قرار می دهیم. در موارد دیگر، مخرج درست بالای صورت نوشته می شد (درست برعکس نماد امروزین ولی بدون خط کسری).
در روم، کسرها در محاسبات مالی و در اندازهگیری ها کاربرد فراوان داشتند. هر کسر نامی خاص داشت و رومی ها معمولاً مخرج کسر را مقدار ثابت 12 می گرفتند؛ این احتمالاً به این دلیل بوده است که سکه ی مسی آن ها، اس (3)، به 12 اونسیا تقسیم می شد. در مدارس روم محاسبات کسری بخش اعظم آموزش حساب را تشکیل می داد.
ظاهراً منشأ شیوه ای امروزینِ نوشتن کسرها هند است. شاید هندی ها این نوع نمایش را از یونان گرفته باشند، چرا که یونانیان در دوره ی متأخر از این شیوه استفاده می کردند. در دست نوشته ی بخشالی (4) (حدود قرن ششم میلادی) کسرها با نوشتن صورت بالای مخرج بدون خط کسری نمایش داده شده اند. اعداد صحیح را به صورت کسرهایی با مخرج 1 نمایش داده اند.
خط کسری حدود اوایل قرن یازدهم میلادی توسط مسلمانان به شکل های زیر به کار می رفت:
اما همه جا از آن استفاده نمی کردند. وقتی که کاهن یهودی، آبراهام بن عِذرا (1907-1167م) شکل مغربی را پذیرفت، معمولاً خط کسری را حذف می کرد، اما در دست نوشته های بعد از آن زمان معمولاً خط کسری وجود دارد.
اولین محرّک استفاده از کسرهای اعشاری را سیمون استون در سال 1585 ایجاد کرد؛ ولی باز هم بسط نمادهای مناسب مدتی به طول انجامید و ممیز اعشاری تا ربع اول قرن هجدهم به طور همگانی استفاده نمی شد.
اکثر نویسندگان کتاب های حساب در اروپا، بحث از کسرهای متعارفی و اعشاری را تا آخر کتاب به تعویق می انداختند. احتمالاً از کمتر خواننده ای انتظار می رفت که به کسرها برسد.
واژه عربی کسر به معنی «شکستن» است. سپس شکل های لاتین fractio و ruptus minutum به معنی «اعداد شکسته» توسط اولین نویسندگان اروپایی به کار رفت که واژه ی انگلیسی fraction به معنی «کسر» از همان ریشه است.
پی نوشت ها :
1.Waldeck E. Mainville/Jr
2. ro
3. s. a
4. Bakhshali
منبع مقاله :
دیویس، هارولد؛ (1384)، تاریخ محاسبه، مهران اخباریفر، تهران، انتشارات علمی و فرهنگی، چاپ اول..
تاریخ کسرها : https://nrich.maths.org/2515
 (یا p / q
(یا p / q  ) از دو عدد صحیح p
) از دو عدد صحیح p  و q
و q  ( به طوری که p
( به طوری که p  صورت کسر و q
صورت کسر و q  مخرج کسر باشد.) بیان شود.[۱] به عبارت دیگر، اعداد گویا کسرهایی هستند که از تقسیم عدد صحیح بر عدد صحیح دیگر (به جز صفر) پدید آمده باشد.[۲] از آنجایی که q
مخرج کسر باشد.) بیان شود.[۱] به عبارت دیگر، اعداد گویا کسرهایی هستند که از تقسیم عدد صحیح بر عدد صحیح دیگر (به جز صفر) پدید آمده باشد.[۲] از آنجایی که q  میتواند برابر با عدد یک باشد؛ پس تمامی اعداد صحیح، طبیعی و حسابی، عدد گویا نیز هستند.
میتواند برابر با عدد یک باشد؛ پس تمامی اعداد صحیح، طبیعی و حسابی، عدد گویا نیز هستند. نمایش داده میشوند که به انتخابِ
نمایش داده میشوند که به انتخابِ  ) بر دیگری (مثلا y
) بر دیگری (مثلا y  ) تقسیم کنیم؛ به طوری که (یا به شرطی که) هم x
) تقسیم کنیم؛ به طوری که (یا به شرطی که) هم x  ) باشند؛ و y
) باشند؛ و y 
 (یعنی متمم اعداد گویا) برابر با مجموعه اعداد حقیقی است؛ و همچنین اشتراک این دو مجموعه برابر با ∅
(یعنی متمم اعداد گویا) برابر با مجموعه اعداد حقیقی است؛ و همچنین اشتراک این دو مجموعه برابر با ∅  (تهی) میباشد :
(تهی) میباشد :

 با اینکه یک کسر است؛ اما یکی از شروط اعداد گویا این است که صورت و مخرج، عددی صحیح باشند؛ در صورتی که صورت یا مخرج، عددی رادیکالی باشد و جذر آن کامل نباشد؛ حاصل رادیکال عددی گنگ خواهد بود. پس این کسر، یک
با اینکه یک کسر است؛ اما یکی از شروط اعداد گویا این است که صورت و مخرج، عددی صحیح باشند؛ در صورتی که صورت یا مخرج، عددی رادیکالی باشد و جذر آن کامل نباشد؛ حاصل رادیکال عددی گنگ خواهد بود. پس این کسر، یک  یک عدد گویا میباشد؛ زیرا حاصل صورت این کسر جذر کامل میباشد.
یک عدد گویا میباشد؛ زیرا حاصل صورت این کسر جذر کامل میباشد. میشود.) بنابراین میتوانیم با دادن عدد یک به مخرج هر یک از آنها کسری داشته باشیم که تمامی شرایط یک عدد گویا را دارد؛
میشود.) بنابراین میتوانیم با دادن عدد یک به مخرج هر یک از آنها کسری داشته باشیم که تمامی شرایط یک عدد گویا را دارد؛ ⇒
⇒  x ∈ Z
x ∈ Z  , n ∈ N
, n ∈ N 
 و c d
و c d  بهصورت زیر مخرجها یکی میشوند:
بهصورت زیر مخرجها یکی میشوند:

 و 3 7
و 3 7  بهصورت زیر مقایسه میشوند:
بهصورت زیر مقایسه میشوند:















 و 17 3
و 17 3  ) شامل یک صورت (Numerator) است که بالای خط قرار میگیرد (یا قبل از
) شامل یک صورت (Numerator) است که بالای خط قرار میگیرد (یا قبل از 


 و 9 6
و 9 6  کسر متعارفی هستند، ولی 4 1.2
کسر متعارفی هستند، ولی 4 1.2  و 5 / 3 / 2 / 1
و 5 / 3 / 2 / 1  کسر متعارفی نمیباشند.
کسر متعارفی نمیباشند. را در نظر بگیرید. اگر صورت از مخرج کسر بزرگتر باشد، یعنی داشته باشیم a>b، کسر از یک (واحد) بزرگتر است. در این صورت a b
را در نظر بگیرید. اگر صورت از مخرج کسر بزرگتر باشد، یعنی داشته باشیم a>b، کسر از یک (واحد) بزرگتر است. در این صورت a b  را میتوان به صورت ۰/۱ نشان داد. همچنین کسر a b
را میتوان به صورت ۰/۱ نشان داد. همچنین کسر a b  یا ۰/۶۰ و حتی بهطور خلاصهتر ۰/۶ نشان داد. کسرهای اعشاری را با
یا ۰/۶۰ و حتی بهطور خلاصهتر ۰/۶ نشان داد. کسرهای اعشاری را با  بیانگر مقدار …۰/۳۳۳۳ است.
بیانگر مقدار …۰/۳۳۳۳ است. همان مقدار ۵٪ یا ۰/۰۵ است و 29 100
همان مقدار ۵٪ یا ۰/۰۵ است و 29 100  مقدار ۲۹٪ را نشان میدهد.
مقدار ۲۹٪ را نشان میدهد. یک عدد اعشاری با مقدار اعشار متناوب ایجاد میکنند. ارقام تکرار شده در تناوب عدد اعشاری را دوره گردش مینامند. از آنجایی که مخرج این گونه کسرها دارای عاملهای اول به غیر از ۲ و ۵ هستند، تقسیم صورت بر مخرج، باقیمانده صفر نخواهند داشت.
یک عدد اعشاری با مقدار اعشار متناوب ایجاد میکنند. ارقام تکرار شده در تناوب عدد اعشاری را دوره گردش مینامند. از آنجایی که مخرج این گونه کسرها دارای عاملهای اول به غیر از ۲ و ۵ هستند، تقسیم صورت بر مخرج، باقیمانده صفر نخواهند داشت. و 1 11 = 0.090909...
و 1 11 = 0.090909... 
 از این گونه کسرها محسوب میشود، زیرا مخرج آن به عاملهای ۵ و ۳ تجزیه میشود.
از این گونه کسرها محسوب میشود، زیرا مخرج آن به عاملهای ۵ و ۳ تجزیه میشود.

 آن کسر تعریف نشدهاست.
آن کسر تعریف نشدهاست.






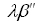 برای 1/32. اما ریاضیدانان یونانی خود را با کسرهای واحد محدود نکردند. گاهی کسرهای کلی را با یک بار نوشتن صورت با یک علامت تکیه و دوبار نوشتن مخرج با دو علامت تکیه نمایش می دادند؛ مثلاً،
برای 1/32. اما ریاضیدانان یونانی خود را با کسرهای واحد محدود نکردند. گاهی کسرهای کلی را با یک بار نوشتن صورت با یک علامت تکیه و دوبار نوشتن مخرج با دو علامت تکیه نمایش می دادند؛ مثلاً،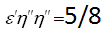 . در بعضی موارد، مخرج را جای می نوشتند که ما امروزه نما را قرار می دهیم. در موارد دیگر، مخرج درست بالای صورت نوشته می شد (درست برعکس نماد امروزین ولی بدون خط کسری).
. در بعضی موارد، مخرج را جای می نوشتند که ما امروزه نما را قرار می دهیم. در موارد دیگر، مخرج درست بالای صورت نوشته می شد (درست برعکس نماد امروزین ولی بدون خط کسری).