 بیان میشود:[۱]
بیان میشود:[۱]بسم الله الرحمن الرحیم
مقطع مخروطی (به انگلیسی: Conic section)، به خمی گویند که از برخورد یک مخروط و یک صفحه حاصل شود.
اثبات اینکه در حالت غیر انحطاط این منحنیها، که به عنوان منحنیهای مکان در صفحه تعریف میشوند، واقعاً به وجود میآیند، میتواند بدون محاسبه با کمک کرههای دندلین انجام شود. اثبات ریاضی در اینجا در مقاطع صفحه بخش مخروط واحد آورده شدهاست. یک مخروط همچنین میتواند به عنوان یک مورد خاص دو بعدی از یک چهارگانه دیده شود و میتوان آن را با یک معادله درجه دوم، معادله مخروطی عمومی توصیف کرد. جاسازی یک بیضی، هذلولی و سهمی در یک صفحه نمایشی منجر به مخروطهای تصویری میشود که همگی معادل یکدیگر هستند، یعنی؛ یعنی میتوان آنها را با نگاشت خط مستقیم به یکدیگر تبدیل کرد.
معادلهٔ یک مقطع مخروطی بهصورت معادلهٔ درجه دو زیر برحسب x , y 
a x 2 + 2 h x y + b y 2 + 2 g x + 2 f y + c = 0

*******************
سایت فرادرس، مقاله دوران مقاطع مخروطی
همانطور که میدانیم، مقاطع مخروطی زمانی تشکیل میشوند که یک صفحه، به گونهای، بخشی از مجموعه دو مخروط را که در رأس با هم مشترک هستند قطع کند. در این آموزش درباره دوران مقاطع مخروطی بحث خواهیم کرد.
شکل زیر، تشکیل بیضی، دایره، هذلولی و سهمی را به خوبی نشان میدهد.
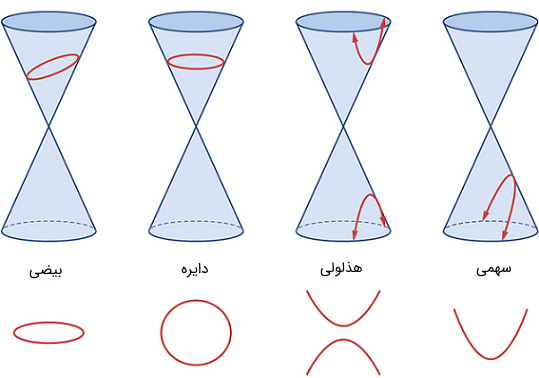
شکل ۱: مقاطع مخروطی ناتباهیده
بیضیها، دایرهها، هذلولیها و سهمیها گاهی مقاطع مخروطی ناتباهیده (Nondegenerate) نیز نامیده میشوند تا با مقاطع مخروطی تباهیده (Degenerate) که در شکل ۲ نشان داده شدهاند تمایز داده شوند. یک مقطع مخروطی تباهیده وقتی ایجاد میشود که یک صفحه دو مقطع را در رأس قطع کند. بسته به زاویه صفحه، سه نوع مقطع مخروطی ممکن است ایجاد شود: یک نقطه، یک خط یا دو خط متقاطع.
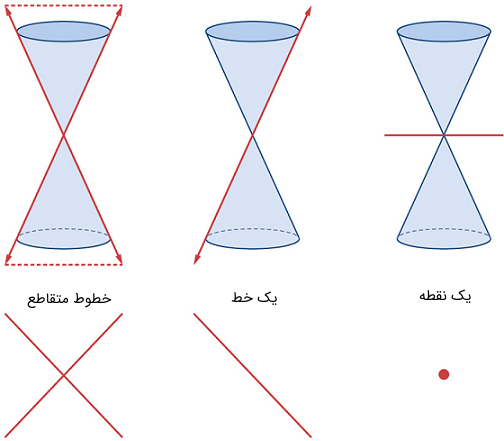
شکل ۲: مقاطع مخروطی تباهیده
***********************
سایت فرادرس، تعریف مقاطع مخروطی و مفاهیم مرتبط با آن
از تقاطع دادن یک صفحه با یک مخروط، میتوان منحنیهای مختلفی از قبیل دایره، بیضی، سهمی یا هذلولی ایجاد کرد. به هر منحنی حاصل از این تقاطع، «مقطع مخروطی» میگویند.
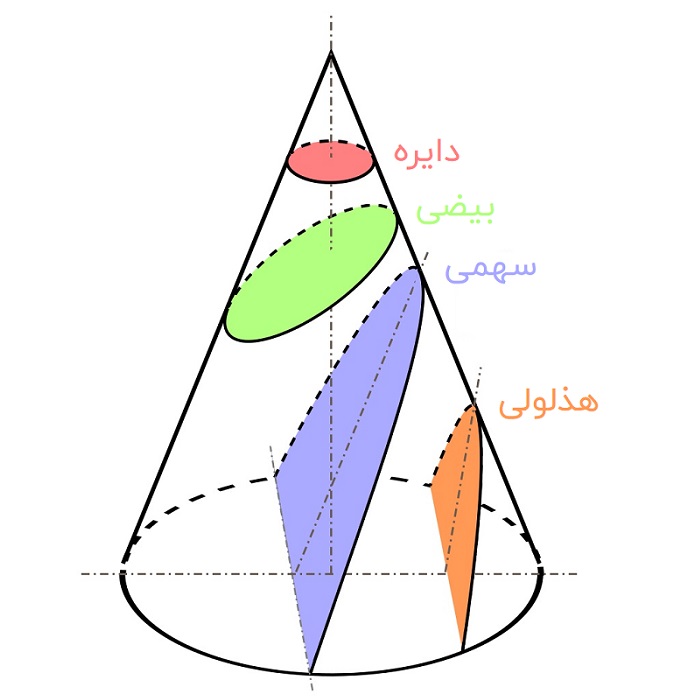
مقاطع مخروطی
این منحنیها را میتوان با استفاده از یک خط راست (خط هادی) و یک نقطه (نقطه کانونی) تعریف کرد. هنگامی که فاصله نقطه کانونی تا یک نقطه بر روی یک منحنی و فاصله عمودی خط هادی تا آن نقطه را اندازهگیری کنیم، نسبت این دو فاصله همیشه یک نسبت ثابت خواهد بود.
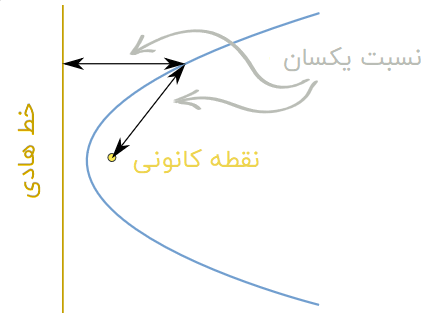
نسبت فواصل در منحنیهای مختلف به صورت زیر است:
نسبتی که در بالا به آن اشاره شد، «خروج از مرکز» نام دارد. با توجه به تعریف خروج از مرکز میتوان گفت: یک مقطع مخروطی، تمام نقاطی است که فاصله آنها تا نقطه کانونی برابر با حاصلضرب خروج از مرکز در فاصله تا خط هادی باشد.
اگر خروج از مرکز،
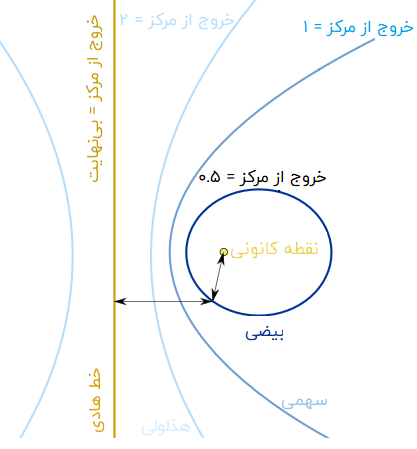
برای یک دایره، خروج از مرکز صفر خواهد بود. در نتیجه، عدد خروج از مرکز، میزان «غیر دایرهای» بودن یک منحنی را نشان میدهد. هر چه خروج از مرکز بزرگتر باشد، انحنا کمتر خواهد بود.
«راست وتر کانونی» (Latus Rectum)، از روی نقطه کانونی میگذرد و با خط هادی موازی است. طول این وتر در مقاطع مخروطی مختلف به صورت زیر است:

در تصویر زیر، قطرهای بزرگ و کوچک یک بیضی را مشاهده میکنید. در اینجا، تنها یک نقطه کانونی و خط هادی وجود ندارد، بلکه در هر طرف بیضی یک جفت از آنها موجود است.

ما میتوانیم معادلهای را ایجاد کنیم که بتواند معرف همهی مقاطع مخروطی باشد.
از آنجایی که این مقاطع، یک سری منحنی مسطح هستند، تنها به دستگاه مختصات کارتزین (استفاده از x و y برای نمایش مختصات نقاط) نیاز خواهیم داشت. از طرف دیگر، چون این منحنیها در خط راست قرار ندارند، باید از عبارتهای زیر نیز در معادله کلی استفاده کنیم:
علاوه بر این، باید برای هر یک از عبارتها، یک ضریب ثابت در نظر بگیریم. با در نظر گرفتن همه اینها، معادله کلی معرف مقاطع مخروطی به صورت زیر درمیآید:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
با استفاده از معادله بالا، میتوان معادلههای دایره، بیضی، سهمی و هذلولی را به دست آورد.
*********************
سایت خوش آموز، مقاله مقاطع مخروطی (Conic Sections)
اگر یک مخروط را بردارید ـــ یکی از آن نان های مخروطی شکل که داخلش بستنی می ریزند را تصور کنید ـــ و آن را از وسط به شیوۀ خاصی برش دهید، لبه های حاصله یکی از چهار مقاطع مخروطی را نشان می دهد: شلجمی (parabola)، دایره (circle)، بیضی (ellipse)، و یا هذلولی (hyperbola).
هر مقطع مخروطی دارای معادلۀ خاصی می باشد، و من هر کدام از آنها را به طور کامل در این فصل پوشش خواهم داد. شما می توانید اطلاعات ارزشمندی را از اینسو و آنسوی یک معادلۀ مقطع مخروطی جمع آوری کنید، اطلاعاتی همچون اینکه، مرکز آن در کجای نمودار است، عرض باز شدن آن چقدر است، و شکل کلی آن به چه شکلی است. همچنین در مورد تکنیکهایی بحث خواهم کرد که، وقتیکه از شما درخواست می شود تا نمودار مخروطی ها را ترسیم کنید، برایتان به بهترین شکل کار کنند.
مقطع مخروطی یک منحنی است که از تقاطع یک مخروط (cone) و یک صفحه (plane) شکل گرفته است (مخروط یک شکل است که پایۀ آن یک دایره می باشد و لبه های آن رو به سمت یک نقطه بهم نزدیک می شوند). منحنی شکل گرفته، بسته به اینکه مخروط از کجایش بریده شود، متفاوت می باشد:
****************
تبیین شهودی و دقیق مقاطع مخروطی با توضیح خط مولد در هندسه ٣ پایه دوازدهم، فصل سوم
إبراهیمُ بنُ سِنان، أبوإسحاق بن ثابت بن قرّة الحرّاني (۲۹۶-۳۳۵/۹۰۹-۹۴۶). طبیب و ریاضي و منجّم شهیر، صابئي المذهب. لیس لدینا معلومات وافیة عن حیاته غیرماقیل إنه ولد ببغداد و نشأ فیها (ابن أبي أصیبعة، ۱/۲۲۶). کان کل من أبیه سنان بن ثابت (ن. ع) وجدّه ثابت بن قُرّة (ن. ع) من علّماء الریاضیات و الأطباء المشهورین في عصرهما – و یبدو أنه درس علی أبیه و علی أساتذة آخرین. و رغم أنه توفي بمرض في الکبد و عمره ۳۹ عاماً، إلا أنه ترک آثاراً عدیدة جعلته من أکبر العلماء و لاسیّما في الریاضیات و النجوم، بحیث استفاد من آثاره عالم البصریات والفیزیائي الکبیر الحسن بن الهیثم أیضاً (م. ن، ۲/۹۴). ویبدو من هذه الآثار أن إبراهیّم کان ینتقد آثار السلف و یتمتّع باستقلال فکري. و یتّضح هذا في الطریقة الجدیدة التي ابتدعها في الحصول علی مساحة القطع المکافئ ومافعله في الساعات الشمسیة وانتقاد لنظریات بطلیموس وأسطو.
هذه بعض مقالاته العلمیة و مصنّفاته:
۱. المقالة في رسم القطوع الثلاثة، و تدور حول رسم مقاطع مخروطیة بایجاد النقط بالمسطرة والفرجار، ولهذه المقالة مخطوطات عدیدة (GAS, V/294) و قد طبعت مع رسائل ابن سنان في حیدرآباد الدکن (۱۳۶۷/۱۹۴۸). و ترجمها إلی الروسیة ج. الدبّاغ و اس. آ. کراسنوا[۱]، و نشرت في مجلة «التاریخ الریاضي، ایسلدوانیا[۲]» (عد 16، موسکو، ۱۹۶۵، ص 447-446).
وقد تمّ البحث بدقّة في هذه المقالة حول رسم القطع المکافئ والقطع الناقص (الاهلیلجي) والطرق الثلاث لرسم القطع الزائد. وهنا نقتصر علی ذکر طریقته في رسم القطع المکافئ: اذا کان عندنا خط L، و نقطتان ثابتتان و متمایزتان علیه N و M (ظ: الشکل ۱)، نختار علیه نقاطاً مثل G, F, E … ثم نرسم أنصاف الدوائر بأقطار ...MG, MF, ME ونقیم أعمدة علی L من النقاط G, F, E, N. فالعمود الذي أقیم من N یقطع أنصاف الدوائر المذکورة بالترتیب في النقاط ..., T, S, R، و نرسم من ..., G, F, E بالترتیب في ..., T۱, S۱, R۱وأثبت إبراهیم بن سنان بالنظر الی أن MN.NE=ER12 و MN.NF=FS12 و MN.NG=GT12 و … بقیاس الخلف أن نقاط ...T1, S1, R1 تقع علی قطع مکافئ برأس N و المحور NQ والوسیط MN، ذلک أن R1 إن لم یکن علی هذا القطع المکافئ مثلاً، فلنفرض أن هذا القطع المکافئ یقطع الخط ER1 في النقطة R3 والتي تختلف عن R۱ کما في الشکل، فیکون والنتیجة أي إن وهذا فیه تناقض. بینما إذا مامددنا کل من لنحصل علی النقاط في الطرف الآخر من الخط ، فإن النقاط المذکورة تقع أیضاً علیهذا القطع المکافئ.
ولابد من الاشارة هنا إلی أن للمقاطع المخروطیة فوائد کثیرة، کصنع المرایا الحارقة، والساعات الشمسیة و غیرها (إبراهیم، «الرسالة الرابعة»).
۲. رسالة في مساحة قطع المخروط المکافئ، و تدور حول معرفة مساحة القطع المکافئ و طریقة الوصول إلی لامساحة المحصورة بین قوس من قطع مکافئ ووتر یصل بین نهایتي القوس. و کان إبراهیم بن سنان قد ألف البدایة رسالة في مساحة هذا القطع. ثم غیر في شکل منه. ولکن النسختین ضاعتا، فاضطرّ إلی إعادة ما استخرجه من ذلک في کتاب آخر لذلک یلفت النظر في المقدمة إلی أنه إن وقعت نسخة لأحد تخالف النسخة الحالیة، فهي احدی النسختین الضائعتین (إبراهیم، «الرسالة الخامس»). وقد طبعت هذه الرسالة مرة في حیدرآباد الدکن (۱۳۶۶/۱۹۴۷). وکذلک حقّهها و ترجمها هاینریش سوتر في ۱۹۱۸م، ونشرها تحت عنوان «رسالة لإبراهیم بن سنان حول مساحة القطع المکافئ» في «المجلة الفصلیة لجمعیة الباحثین في العلوم»۳ (ص ۲۱۴-۲۲۸)، ولایزال عدد من مخطوطات هذه الرسالة موجوداً GAS, V/۲۹۳, ۲۹۴, ۴۰۲؛ کراوزه، ۴۶۱). وقد أُثبتت نظریة أرخمیدس في هذه الرسالة بشکل جدید کمایلي:
الشکل ۱
إذا نظرنا إلی الشکل ۲ فإن النقاط P، N، M تقطع علی قطع مکافئ واحد. والخطالمماس علی القطع المکافئ في النقطة P یوازي الخط MN (نسمّي P رأس هذه القطعة). وتفید هذه القضیة أن مساحة المثلث MNP تساوي ثلاثة أرباع المساحة المحصورة بین الخط MN والقطع المکافئ MNP. وقد أثبت ابن سنان مساحة القطع المکافئ بثلاثة قضایا، وأثبت قضیة الثالثة، والتي هي هذه النتیجة، مباشرة، أي بالإستفادة من قضیة الثانیة: [إذا کانت: Ai مساحة قطعة من القطع المکافئ، و Bi مساحة ذلک المثلث الذي قاعدته هي قاعدة القطعة المذکورة و رأسه رأسها فإن . بینما أثبت أرخمیدس مساحة القطع المکافئ بسبع قضایا و بناء علی قیاس الخلف. والجدیر بالذکر أن أرخمیدس وصل إلی هذه النتیجة بطریقة عملیة أولاً ثم بالبرهان السابق.
أبو الجود، محمد بن اللّيث (ق 4 ه/ 10 م)
هو محمد بن الليث، أبو الجود، أحد كبار الرياضيين الذين عرفهم القرن الرابع ه/ 10 م، و يعتقد أنّه من بلاد فارس، لكنّ حياته ظلّت مجهولة لدى المؤرّخين إذ لا يعرفون عنها سوى أنّ صاحبنا قد عاش في عصر العالم أبي الريحان البيروني (362 ه/ 973 م- حوالي 440 ه/ 1048 م) مستنتجين ذلك من المراسلات التي اكتشفوها بين الرجلين. و المؤرّخون واثقون أيضا بأنّ أبا الجود سبق عمر الخيام (ت 515 ه/ 1121 م) في التأليف لأنّ هذا الأخير تناول بعض كتاباته و وصف صاحبها ب «المهندس الفاضل». و أشار عمر الخيام إلى أنّ أبا الجود حل مسألة جبريّة تؤدي إلى معادلة تكعيبية لم يتمكن من حلها معاصروه.
كان عمر الخيام شاعرا و فلكيا و رياضيا بارزا.
و من بين اكتشافاته في الرياضيات طريقة هندسية لحل معادلات تكعيبية يستخدم فيها تقاطع الدوائر مع ما يعرف في الهندسة بالقطوع المكافئة. و كان جانب من هذه الطريقة قد تمّ وصفه من قبل رياضيين سابقين، نجد من بينهم، بوجه خاص، أبا الجود.
موسوعة أعلام العلماء و الأدباء العرب و المسلمين، ج5، ص: 521
و قد تكرّر ذكر أعمال أبي الجود على لسان عمر الخيام، سيما رسالته في تعداد أصناف المعادلات. و من المعلوم أنّ عمر الخيام اطلع عليها بطريقة غير مباشرة حيث يقول:
«و قد حكي لي ... أنّ لأبي الجود ...
كلاما ...». و يقول عمر الخيام في معرض حديثه عن إحدى المسائل الرياضيّة:
«... و المسألة التي أعجزت أبا سهل الكوهي، و أبا الوفاء البوزجاني، و أبا حامد الصاغاني و جماعة من أصحابهم الذين كانوا منقطعين إلى جانب الدولة بمدينة السلام هي ... و هؤلاء الأفاضل كانوا متحيرين في هذه المسألة مدّة مديدة استخرجها أبو الجود، و خزنوها في دار كتب الملوك السامانية ...» [رشدي راشد، جبّار أحمد، رسائل الخيام الجبريّة، ص 91].
و كشف عمر الخيام عن بعض أخطاء أبي الجود إذ يقول: «... فقد ظهر خطأ أبي الجود في قوله إنّ القطعين لا يتلاقيان و ذلك المراد». و في مكان آخر يلاحظ الخيام:
«... و بعد فإن واحدا من أصحابنا اقترح علينا أن نبيّن خطأ أبي الجود محمد بن الليث في الصنف الخامس من الأصناف الستة الثلاثية التي تنحل بالقطوع ... قال أبو الجود ... ثم زعم أن القطعين يتماسان في نقطة ... و أخطأ لأنّه يجب أن يكونا متقاطعين» [المرجع السابق، ص 73، 76].
و نجد عمر الخيام يتحدّث عن مسألة تسمى «مسألة أبي الجود بن الليث» فاستهل بالقول:
«هذا و قد حكى لي بعض من شدا شيئا نزرا من الهندسة بعد تأليفي هذه الرسالة بخمس سنين أنّ لأبي الجود محمد بن الليث المهندس كلاما في تعديد هذه الأصناف و تحليل أكثرها إلى القطوع المخروطيّة من غير استيفاء جميع أنواعها و تمييز الممكن من المستحيل، بل بحسب ما تؤدّي به النظر في المسائل الجزئيّة إليها فلم أستبعد ذلك لأنّ هذين الصنفين اللذين نسبتهما إلى واحد ممّن تقدّمنا منسوبان إليه و قد شاهدتهما و تصفحتهما في جملة تصنيفات أبي الجود بخط الحازمي الخوارزمي ...» [المرجع السابق، ص 72].
و يعترف عمر الخيام- بخصوص هذه المسألة- بفضل أبي الجود حيث ينوه به قائلا:
«... فلعمري إنّه قد أحسن في الوقوف على هذه المسألة بعد ما أعيت جماعة من المهندسين لكن مسألته جزئيّة».
و قد أسهم أبو الجود في مجال الحساب في البحث عن حل للمسألة التي عرفت فيما بعد بمخمنة فيرما tamreF (1601- 1665) (رياضي فرنسي من القرن السابع عشر)، و التي لم تعرف حلّها النهائي إلّا في أواخر القرن العشرين على يد الرياضي الانجليزي اندريو وايلز seliW عام 1994. و يذكر المؤرّخ الغربي المعاصر لين برغرين nerggreB الذي درس بعض أعمال أبي الجود أنّ معظم مؤلفات هذا الرياضي لم تكتشف بعد، معتمدا في الحكم على الإحالات إلى أعماله التي نجدها في الكتابات الأخرى.
و من جهة أخرى يلاحظ مؤرّخ الرياضيات العربيّة رشدي راشد أنّ اللجوء إلى هندسة القطوع المخروطيّة بهدف دراسة المعادلات التكعيبيّة و تعيين جذورها سرعان ما اتبعه
موسوعة أعلام العلماء و الأدباء العرب و المسلمين، ج5، ص: 522
العلماء العرب و المسلمون، و من بينهم أبو الجود. و كان هذا الإسهام قد توّج بإسهام عمر الخيام. كما أشار رشدي راشد في هذا السياق إلى أنّ أبا الجود قد درس المثلثّات في رسالة عن المثلّثات القائمة الزاوية، و أنشأ جداول لتسجيل أضلاع المثلّثات الناتجة و مساحاتها، و نسبة هذه المساحات إلى المحيطات، و ذلك انطلاقا من ثنائيّات أعداد صحيحة.