بسم الله الرحمن الرحیم

سهمی

سایت ویکی پدیا

در ریاضیات سَهمی (به انگلیسی: Parabola) مکان هندسی نقاطی از صفحه است که از یک خط و از یک نقطه هم فاصله هستند. این منحنی که شَلجَمی یا شَلغَمی^[۱] هم نامیده می‌شود یکی از مقاطع مخروطی می‌باشد، زیرا از تقاطع یک صفحه و یک مخروط می‌تواند به وجود بیاید.^[۲] سهمی و هذلولی دو مقطع مخروطی باز هستند و بیضی و دایره دو مقطع مخروطی بسته.

تاریخچه

یونان باستان

بنابر تقریظی از اراتوستن، سهمی را نخستین‌بار منایخموس (۳۸۰ — ۳۲۰ پ. م)، دوست نزدیک افلاطون، در تلاش برای حل تضعیف مکعب (ساختن مکعبی که حجم آن دو برابر حجم یک مکعب مفروض است فقط با استفاده از خط‌کش و پرگار) کشف کرد. آپولونیوس برای اولین بار نام «پارابول» (یونانی: παραβολή، به معنای «کاربرد»)^[الف] را بر روی سهمی گذاشت^[۳] و اقلیدس (حدود ۳۶۵–۲۷۵ پ. م) بررسی دقیقی از ویژگی‌های سهمی ارائه کرد.^[۴] پاپوس اسکندرانی (حدود ۳۵۰ — ۲۹۰ پ. م) مفهوم خط‌های هادی را برای نخستین بار بررسی کرد و نشان داد که هر منحنی نسبت ثابتی (که بعدها به برون‌مرکزی معروف شد) دارد و این نسبت ثابت برای همهٔ سهمی‌ها برابر ۱ است.^[۵]

نام آپولونیوس (اواخر قرن سوم — اوایل قرن دوم پیش از میلاد) برای قرن‌ها پس از مرگ او با مطالعهٔ مقاطع مخروطی گره خورده بود. آپولونیوس اثر مهمش «مخروطات» را، که مشتمل بر هشت مقاله است،^[۶] با مطالعهٔ مخروط آغاز می‌کند و پس از تعریف سه مقطع مخروطی (سهمی، هذلولی، و بیضی)، به تعریف خط مماس آن‌ها می‌پردازد و سپس ثابت می‌کند که فاصلهٔ کانونی برای همهٔ نقاط روی یک بیضی ثابت است.^[۷]

قرون وسطی

همزمان با حکومت مأمون در خراسان (در قرن سوم هجری)، اخوان ثلاثهٔ بنوموسی دست به ترجمهٔ مخروطات آپولونیوس از یونانی به عربی زدند. بنوموسی فقط نسخه‌ای ناقص از مخروطات را در اختیار داشتند و مقاطع مخروطی در زمان ایشان به دست فراموشی سپرده شده بود، بنابراین در فهم متن دچار مشکل بودند. اندکی بعد، یکی از اخوان ثلاثه به نام حسن نظریهٔ مقاطع استوانه‌ای را ابداع کرد که می‌توان آن را مقدمه‌ای ساده بر مقاطع مخروطی دانست. پس از درگذشت حسن، برادرش احمد در شام نسخه‌ای کامل‌تر از چهار فصل اول مخروطات را با شرح اوتوکیوس پیدا کرد و به کمک برادر دیگرش، محمد، و با استفاده از دو نسخهٔ موجود و نظریهٔ حسن، موفق شد نظریات آپولونیوس را دریابد. احمد و محمد ترجمهٔ مقالهٔ اول تا چهارم مخروطات را به هلال حمصی و مقالهٔ پنجم تا هفتم آن را به ثابت بن قره سپردند و خود بازنگری نهایی ترجمه را عهده‌دار شدند. ترجمهٔ برادران بنوموسی از مقالات پنجم تا هفتم مخروطات تنها نسخهٔ باقی ماندهٔ این اثر است.^[۶] ترجمهٔ آثار علمی به عربی اغلب نیازمند ابداع اصطلاحات فنی تازه بود و مترجمان آن‌ها، بر خلاف مترجمان لاتین، به ترانویسی عبارات یونانی اکتفا نکردند^[ب] و برای واژهٔ «پارابولی» اصطلاح «مکافی» را در نظر گرفتند که معنای آن را حفظ می‌کند^[پ] و هنوز در زبان عربی به بیضی «قطع ناقص» گفته می‌شود.^[۶]

رنسانس و قرون جدید

اسحاق نیوتن در کتاب «اصول ریاضی فلسفه طبیعی»^[۸] نشان داد که اگر نیروی کشش میان اجسام آسمانی متناسب با معکوس مجذور فاصله بین آن دو باشد، اجرامی که به دور یک جرم بزرگ می‌گرداند، یا باید حرکت دایره‌ای، بیضوی، سهموی یا هذلولوی داشته باشند. نیوتن از سهمی برای محاسبه مدار شهاب سنگ‌ها استفاده کرد.^[۹] امروزه می‌دانیم که اگر چه سهمی مدل خوبی برای حرکت شهاب سنگ‌ها می‌باشد ولی این مدل از دقت بالایی برخوردار نیست و به ندرت مدار شهاب سنگ‌ها با دقت بسیار بالایی سهموی می‌باشند.^[۱۰]

گالیله نشان داد که وقتی جسمی را در هوا پرتاب می‌کنیم، مسیر حرکت آن سهموی می‌باشد.^[۱۱] این موضوع زمانی صحت دارد که از مقاومت هوا و آثار چرخشی چشم پوشی شود.^[۲]

نیوتون و گرگوری نشان دادند که هنگامی که نور به صورت موازی به یک آینه سهموی تابانده شود، پس از انعکاس در کانون آن جمع می‌شود.^[۱۱]

پاسکال سهمی را تصویر یک دایره در نظر گرفت.^[۱۱]

رنه دکارت خود مقاطع مخروطی آپولونیوس، به‌ویژه بیضی و سهمی، را در آثارش در باب هندسه تحلیلی بررسی کرده بود.^[۱۲]

پس از نیوتن

کاربرد

اقتصادی‌ترین شکل پل کمانی در اغلب شرایط عملی سهمی می‌باشد.^[۱۳]

تعریف سهمی

سهمی به عنوان مقطع مخروطی

سهمی خمی باز است که از برخورد مخروطی قائم با قاعدهٔ دایره‌ای و صفحه‌ای حاصل می‌شود که با یکی از وترهای مخروط موازی باشد ولی با ارتفاع مخروط موازی نباشد.^[۱۴] اگر این صفحه با قاعدهٔ مخروط موازی باشد حاصل دایره، اگر با ارتفاع مخروط موازی باشد حاصل هذلولی، و اگر با هیچ‌یک از وترهای مخروط یا ارتفاع آن موازی نباشد حاصل بیضی خواهد بود.^[۱۵]

تعریف سهمی به صورت مکان هندسی نقاط

در صفحهٔ اقلیدسی سهمی را می‌توان به صورت مجموعه ای از نقاط (مکان هندسی) تعریف کرد.

سهمی مکان هندسی نقاطی است که فاصلهٔ آن‌ها از نقطه ای ثابت به نام کانون با فاصلهٔ آن از خط ثابتی به نام خط هادی برابر باشد.

^{${\displaystyle \{P:|PF|=|Pl|\}}$}

معادله

معادله ساده سهمی:${\displaystyle y=x^{2}\,}$ می‌باشد. شکل کلی معادله سهمی در دستگاه مختصات دکارتی، به شکل زیر است:

${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0\,}$

که ضرایب ${\displaystyle A}$ تا ${\displaystyle F}$ همگی ثابت و حقیقی بوده، ${\displaystyle A}$ یا ${\displaystyle C}$ غیر صفر هستند، و همچنین ${\displaystyle B^{2}=4AC\,}$.

مختصات قطبی

مقاطع مخروطی با کانون مشترک

اگر p > 0 سهمی ای با معادلهٔ دکارتی ${\displaystyle y^{2}=2px}$ (سهمی به سمت راست باز می‌شود) دارای معادلهٔ قطبی زیر است:

${\displaystyle r=2p{\frac {\cos \varphi }{\sin ^{2}\varphi }},\quad \varphi \in \left[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right]\setminus \{0\}}$

(${\displaystyle r^{2}=x^{2}+y^{2},\ x=r\cos \varphi }$).

محور سهمی ${\displaystyle V=(0,0)}$ و کانون آن ${\displaystyle F=\left({\tfrac {p}{2}},0\right)}$ است.

اگر مبدأ را به سمت کانون جابه جا کنیم یعنی ${\displaystyle F=(0,0)}$ معادله ی قطبی زیر را خواهیم داشت:

${\displaystyle r={\frac {p}{1-\cos \varphi }},\quad \varphi \neq 2\pi k.}$

روش انتقال

${\displaystyle y=a(x-h)^{2}+k\,}$

• a بیانگر باز و بسته شدن دهانه تابع است.
• h بیانگر جابجا شدن نمودار در جهت افقی. (برخلاف علامت h حرکت می‌کند)
• k بیانگر جابجا شدن نمودار در جهت عمودی. (برجهت علامت k حرکت می‌کند)

در معادله بالا h باعث انتقال افقی و k باعث انتقال عمودی می‌شود. کافیست نمودار ${\displaystyle y=x^{2}}$ رسم کرده و با توجه به علامت h و k آن را منتقل می‌کنیم.

انتقال سهمی

خاصیت بازتاب نور

نورهایی که موازی با خط قرینه سهمی وارد سهمی می‌شوند، به کانون بازتاب می‌کنند.

خاصیت بازتاب سهمی بیان می‌دارد که اگر یک سهمی آیینه ای باشد و بتواند نور را بازتاب کند، آنگاه نورهایی که موازی با خط تقارن سهمی به آن وارد می‌شوند، به سمت کانون آن بازتاب می‌کنند.

اثبات

در شکل مقابل F نقطه کانون سهمی، P نقطه ای دلخواه روی سهمی، PT عمودی بر خط هادی سهمی و MP نیم ساز زاویه FPT∠ است. Q نقطه ای دیگر روی سهمی است و QU نیز عمود بر خط هادی است. ما می‌دانیم FP = PT و FQ = QU. به وضوح، QT > QU, پس QT > FQ. اما از طرفی تمام نقاط روی MP از F و T به یک فاصله هستند. یعنی هیچ نقطه ای روی سهمی نیست که روی MP باشد؛ که یعنی خط مماس به سهمی که از نقطه T می‌گذرد، نیمساز FP و PT است. با توجه به این که زاویه تابش نور از خط مماس به منحنی با زاویه بازتاب برابر است، می‌توان دریافت که پرتو بازتاب در راستای همان خطی است که به F می‌رود.

ویژگی‌ها

• معادلهٔ سهمی در یک سیستم مختصات تخصیص‌یافته عبارت است از ${\displaystyle x^{2}-2py=0}$. رأس این سهمی در ${\displaystyle O(0,0)}$ قرار دارد و محور ${\displaystyle y}$ها محور تقارن آن است.^[۱۶]
• نقطه تمرکز ${\displaystyle F(0,p/2)}$ سهمی بر روی محور تقارن قرار دارد و گسترندهٔ سهمی (منحنی مکان هندسی مرکز انحناهای آن) تنها یک نوک تیز دارد.^[۱۷]
• خط تمرکز معادل ${\displaystyle f:y=-p/2}$ است که عمود بر محور ${\displaystyle x}$ها است و فاصله‌اش از نقطهٔ تمرکز (${\displaystyle F}$) برابر ${\displaystyle p}$ است.^[۱۸]
• برای هر نقطهٔ ${\displaystyle q}$ روی سهمی، فاصلهٔ ${\displaystyle q}$ از نقطهٔ تمرکز ${\displaystyle F}$ فاصلهٔ آن از خط تمرکز ${\displaystyle f}$ است.^[۱۹]
• همهٔ سهمی‌ها با هم متشابه‌اند.^[۲۰]
• سهمی‌هایی با ${\displaystyle p}$ برابر با یکدیگر همنهشتند.^[۲۱]
• فرمول پارامتریک سهمی: نمونهٔ آن می‌تواند ${\displaystyle c(t)=(t,t^{2}/2p)}$ باشد.^[۲۲]

رسم سهمی

معادله درجه دو ${\displaystyle y=ax^{2}+bx+c\,}$ را در نظر می‌گیریم. برای رسم سهمی کافیست که راسش را پیدا کنیم.

فرمول راس سهمی برابر است با:

${\displaystyle (-{\frac {b}{2a}},-{\frac {\Delta }{4a}})\,}$

حال ما راس را داریم و دو نقطه دیگری را با جایگذاری در فرمول پیدا کرده و نمودار را رسم می‌کنیم.

نکته: اگر در معادله درجه دو a مثبت باشد دهانه سهمی رو به بالا و اگر منفی باشد دهانه سهمی رو به پایین است.

**************************

**************************

سایت فرادرس-مقاله منحنی سهمی

تعریف منحنی سهمی

هنگامی که شما به یک توپ فوتبال ضربه می‌زنید (یا تیری را از کمان رها کرده یا سنگی را به سمت آسمان پرتاب می‌کنید) پرتابه با طی کردن یک کمان به سمت بالا رفته و سپس سقوط می‌کند. مسیر پیموده‌شده توسط پرتابه بخشی از یک منحنی «سهمی» (Parabola) می‌باشد.

ساختار منحنی

سهمی نوعی منحنی می‌باشد که فاصله هرنقطه روی آن از نقطه ثابت (کانون) و خط ثابت (خط هادی) مقداری برابر است.

کاغذی تهیه کنید، خطی مستقیم روی آن ترسیم کنید سپس نقطه ای به عنوان کانون (در مکانی غیر از روی خط هادی) ایجاد نمایید. اکنون با آزمون و خطا نقاطی را روی صفحه بیابید که از کانون و خط هادی فاصله‌ای برابر داشته‌باشند. سپس این نقاط را به یکدیگر متصل نمایید. اکنون شما یک منحنی سهمی دارید!

آشنایی با بخش‌های مختلف یک سهمی

در ادامه شما را با تعدادی از اجزای اصلی این منحنی آشنا خواهیم کرد:
• خط هادی و کانون (در بالا شرح داده‌شده‌است.)
• محور تقارن (با عبور از کانون، بر خط هادی عمود می‌گردد.)
• رأس (نقطه‌ای که سهمی بیشترین پیچش خود را دارد و دقیقا میان کانون و خط هادی قرار دارد.)

سهمی منعکس کننده است

حیرت‌آورترین ویژگی یک سهمی این است که هر پرتویی موازی با محور تقارن سهمی به آن تابیده شود پس از بازتاب از کانون عبور می‌کند. دلیل نامگذاری این نقطه نیز به خاطر همین ویژگی است. زیرا تمامی پرتو‌ها در این نقطه متمرکز می‌شوند.

بنابراین از سهمی‌ها می‌توان در موارد زیر استفاده نمود:
• دیش‌های ماهواره
• دیش‌های رادار
• متمرکزسازی تشعشعات خورشیدی جهت ایجاد یک نقطه‌ با دمای بالا
• ایجاد سطح بازتاب‌کننده روی نور افکن‌ها و چراغ‌قوه‌ها

همچنین با برش یک مخروط به‌وسیله یک صفحه (صفحه باید با سطح مخروط موازی باشد.) نیز می‌توان به یک سهمی دست‌پیدا‌نمود. بنابراین منحنی بدست‌آمده مقطعی از یک مخروط است.

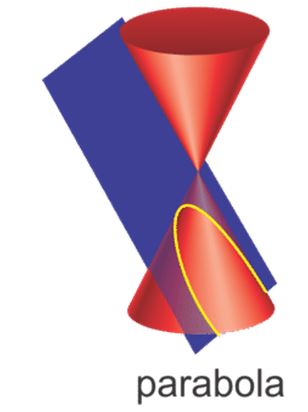 معادلات سهمی

ساده‌ترین معادله برای یک سهمی y = x^2 است.

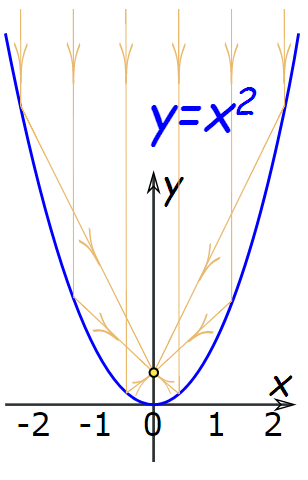
با قراردادن توان 2 در سمت چپ معادله (y^2=x) شکل منحنی به صورت زیر می‌شود.

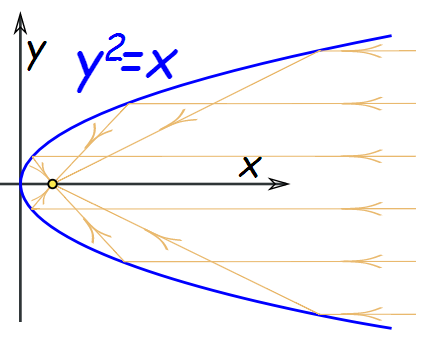
در حالت کلی‌تر: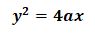

که a همان فاصله کانون از مبدأ مختصات می‌باشد.

مثال: فاصله کانونی را در معادله زیر بیابید.

با تبدیل معادله y^2 = 5x به فرم کلی y^2 = 4ax داریم: y^2 = 4 (5/4) x
که مقدار a = 5/4 بدست می‌آید. پس برای معادله سهمی y^2 = 5x :

F = (a,0)

معادلات سهمی‌ها با جهت‌گیری‌های مختلف در شکل زیر نشان‌داده‌شده‌است:

محاسبات موردنیاز برای ساخت دیش سهمی

درصورتی که تمایل به ساخت یک دیش با نقطه کانونی 200mm بالای سطح داشته‌باشید به چه محاسباتی نیاز دارید؟

برای ساده‌تر کردن فرآیند ساخت آن بیاید جهت گیری دیش را به سمت بالا درنظر بگیریم. به همین منظور باید از معادله x^2 = 4ay استفاده نماییم. در این معادله مقدار a را 200 قرار می‌دهیم. پس معادله‌ به شکل زیر در‌می‌آید:

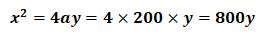
با یک عملیات جبری ساده می‌توانیم ارتفاع دیش را در نقاط مختلف محاسبه کنیم:

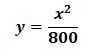
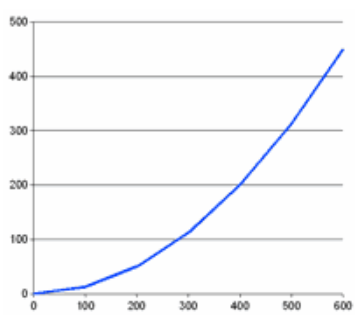
ارتفاع دیش را در فواصل افقی مختلف به سادگی می‌توانیم بدست آوریم:

تلاش کنید خودتان در منزل نمونه‌ای از آن را بسازید. سرگرم‌کننده خواهد بود! فقط به این نکته توجه کنید که، یک سطح منعکس کننده می‌تواند حرارت زیادی را متمرکزکند.

اگر تمایل به مطالعه بیشتر در مورد این موضوعات را داشته باشید؛ شاید آموزش های زیر نیز برای شما مفید باشند:

• سطح مقطع در هندسه — به زبان ساده
• تعریف حلقه و محاسبات آن در هندسه — به زبان ساده
• حرکت انتقالی در ریاضیات — به زبان ساده
• تقارن چرخشی در اشکال دوبعدی — به زبان ساده

پیشنهاد یا مطلب تحقیقی یا ویرایشی یا هر نوع چیزی که مناسب میدانید ارسال فرمایید تا به متن فعلی فورا ضمیمه شود.