بسم الله الرحمن الرحیم
لینک کتاب در سایت طاقچه
لينك نسخه خطی کتاب در سایت کتاب بدیا(این کتاب شامل هشت رساله است که رساله چهارم آن، رساله محیطیه می باشد)
الحمدلله العالم بنسبة القطر الی المحیط العارف بمقدار کل المرکب و البسیط خالق الارض و السموات جاعل النور فی الظلمات و الصلوة و السلام علی محمد المصطفی مرکز دائرة الرسالة و محیط اقطار الهدایة و العدالة و علی آله الطیبین و اصحابه الطاهرین اما بعد فیقول احوج خلق الله تعالی الی غفرانه جمشید بن مسعود بن محمود الطبیب الکاشانی الملقب بغیاث احسن الله احواله ...
سایت دائرة المعارف بزرگ اسلامی
رِسالِۀ مُحیطیّه،رسالهای مهم دربارۀ محاسبۀ نسبت محیط دایره به قطر آن (عدد π)، نوشتۀ غیاثالدین جمشید کاشانی (ه م)، در اواسط شعبان ۸۲۷/ ژوئیۀ ۱۴۲۴.
این رساله دارای یک مقدمه، ۱۰ فصل و خاتمه است:
کاشانی در این مقدمه با یادکرد تقریبهای بهدستآمده توسط پیشینیان برای عدد π، در هر مورد خطای ناشی از بهکارگیری هر تقریب در محاسبۀ محیط دایرههای بسیار بزرگ مانند دایرۀ عظیمۀ کرۀ زمین و فلکالبروج را محاسبه، و اشتباهات احتمالی آنان در مراحل محاسبه را نیز گوشزد کرده است که عبارتاند از:
۱. تقریب بهدستآمده توسط ارشمیدس با محاسبۀ محیط دو ۹۶ضلعی منتظم (نک : گ ۱ ب -۲ آ)؛
۲. تقریب ابوالوفای بوزجانی با محاسبۀ محیط ۷۲۰ضلعی منتظم محاطی و محیطی (گ ۲ آ)؛
۳. تقریب ابوریحان بیرونی با محاسبۀ میانگین محیط ۱۸۰ضلعی منتظم محاطی و محیطی (گ ۲ آ-۲ ب).
براساس گزارش کاشانی، ارشمیدس، بوزجانی و بیرونی (ه م م)، همگی در یافتن تقریبی برای عدد π محیط دو nضلعی منتظم، یکی محاط در و دیگری محیط بر دایره، را به دست آوردهاند که محیط دایره از اولی بزرگتر، و از دومی کوچکتر است و معمولاً میانگین این دو را محیط دایره انگاشته، و با تقسیم آن بر شعاع قطر یا شعاع دایره، مقدار π یا ۲π را یافتهاند که هرچه n بزرگتر باشد، میتوان به تقریبی بهتر دست یافت. کاشانی نیز از همین روش پیروی کرده، با این تفاوت که برای رسیدن به دقت دلخواه، n را بسیار بزرگتر از پیشینیان خود در نظر گرفته است. او در پایان این مقدمه، هدف خود را یـافتن تقریبی برای عدد π در نظر گرفته است که خطای حاصل از بهکارگیری آن در محاسبۀ دایرهای که قطرش ۶۰۰هزار برابر قطر زمین باشد، کمتر از مویی باشد. درواقع، کاشانی در پی رسیدن به دقتی است که خطای محاسبۀ او برای محاسبۀ بزرگترین دایرۀ قابل ترسیم در جهان هستی ــ که مطابق هیئت قدیم، شعـاع دایرۀ عظیمۀ کرۀ عالم است ــ به کوچکترین واحد اندازهگیری در آن روزگار، یعنی قطر یک مو نرسد (گ ۱ ب - ۲ ب؛ نیز نک : لوکای، 40-47 ,3-4؛ قربانی، ۱۳۳-۱۳۷؛ هوخندایک، 76-78؛ آذریان، «مقدمه [۱]... »، 907-912).
موضوع این فصلها بدین قرار است:
۱. در تعیین وتر مجموع یک کمان و نصف مکمل آن. در این بخش، غیاثالدین کاشانی قضیهای را مطرح میکند که پایۀ محاسبات فصلهای بعدی است:
در نیمدایرهای به مرکز O و شعاع r اگر قطر AB را رسم کنیم و نقطۀ G را بهدلخواه روی آن انتخاب کنیم و وسط کمان GB را D بنامیم، رابطۀ زیر برقرار خواهد بود:
(۱) r(۲r+AG)=AD۲
پس اگر شعاع دایره و وتر AG معلوم باشند، وتر AD بهسادگی به دست خواهد آمد (همانجا؛ نیز نک : لوکای، 47-49 ,4-5؛ قربانی، ۱۴۳؛ هوخندایک، 78؛ آذریان، «قضیه [۲]... »، 499-502).
اگر r را یک بگیریم و اندازۀ کمان AG برحسب رادیان را ۲þ بنامیم، خواهیم داشت:
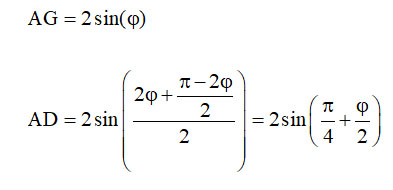
درنتیجه، حکم قضیه بهصورت زیر در خواهد آمد:
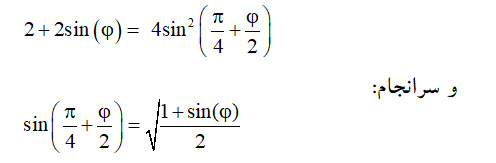
این همان رابطهای است که اروپاییان در ۱۷۷۰م (۳۴۶ سال پس از کاشانی)، و توسط یوهان هاینریش لامبرت [۳]برای نخستینبار بدان دست یافتند (نک : لوکای، 49؛ قربانی، ۱۴۴).
۲. در تعیین محیط چندضلعیهای منتظم محاطی و محیطی.
در این فصل، کاشانی نخست با درنظرگرفتن وتر کمان ۶۰ درجه، و استفادۀ پیاپی از قضیۀ فصل نخست، بهترتیب، وتر کمانهای ۱۲۰، ۱۵۰، ۱۶۵، ۵/ ۱۷۲ درجه را به دست میآورد:
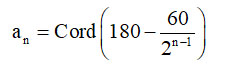
اگر وتر کمانهای مکمل این زوایا را cn بنامیم، خواهیم داشت:
(۲)
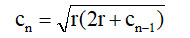
ازآنجاکه وترهای دو کمان متمم (an و cn) یک مثلث قائمالزاویه تشکیل میدهند، خواهیم داشت:
(۳)
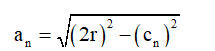
که در آن، an، ضلع یک 3×2n ضلعی منتظم محاطی است (گ ۲آ-۳آ؛ نیـز نک : لـوکـای، 50-54 ,5-6؛ قـربـانـی، ۱۴۴-۱۴۶؛ هوخندایک، 78).
۳. در محاسبۀ حداقل مقدار n، برای آنکه خطای محتمل در محاسبۀ محیط دایره از مقداری مطلوب کمتر باشد. کاشانی برای رسیدن به دقت مطلوب خود (خطای کمتر از یک مو در اندازهگیری دایرۀ عظیمۀ کرۀ عالم) به این نتیجه میرسد که شمار اضلاع 3×2n ضلعیهای منتظم محاطی و محیطی باید چندان باشد که تفاوت میان محیط این دو از ۸ رابعه (8/ 604) کمتر باشد، که از آنجا مقدار ۲۸=n را به دست میآورد (گ ۴ آ -۵ ب؛ نیز نک : لوکای، 54-59 ,6-8؛ قربانی، ۱۴۶-۱۴۷؛ هوخندایک، همانجا).
۴. در محاسبۀ وتر کمانهای مکمل 3×2n ضلعی براساس دستور شمارۀ ۲ (گ ۵ ب ـ ۲۰ آ): این بخش مفصلترین و مهمترین بخش رسالۀ محیطیه است. همانگونه که از رابطۀ محاسبۀ cn پیدا ست، دقت محاسبه بستگی تام به میزان دقت استخراج ریشۀ دوم در این رابطه دارد. کاشانی به این نتیجه میرسد که برای رسیدن به دقت مطلوب، باید هر عمل جذرگیری را با ۲۰ رقم شصتگانی (دو رقم صحیح و ۱۸ رقم کسری) انجام دهد. در این فصل، برای بهدستآوردن cnها (n از ۱ تا ۲۸)، جدولهایی برای محاسبۀ جذر در دستگاه شمار شصتگانی آمده است (لوکای، 59-64,8-15؛ قربانی، ۱۴۸- ۱۴۹؛ هوخندایک، همانجا).
۵. در بهدستآوردن اندازۀ ضلع چندضلعی منتظم محاط در دایره با شمار ضلعهای «ا ب ح یو یب مح» (یعنی ۱، ۲، ۸، ۱۲، ۱۶، ۴۸) در دستگاه شمار شصتگانی برابر ۲۲۸×۳ = ۳۶۸‘۳۰۶‘۸۰۵، از دستور شمارۀ ۳ (گ ۲۰ ب؛ نیز نک : لوکای، 64 , 16؛ قربانی، ۱۴۹- ۱۵۰؛ هوخندایک،78-79).
۶. در بهدستآوردن محیط چندضلعیهای منتظم محاط و محیط بر دایره که شمار ضلعهای آن ۳۶۸‘۳۰۶‘۸۰۵ باشد. کاشانی محیط چندضلعیهای محاطی و محیطی یادشده را با فرض یکبودن شعاع دایره در دستگاه شصتگانی عرضه میکند که مقدار ۲π میانگین این دو مقدار خواهد بود:
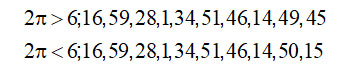
همانطور که او از پیش انتظار داشت، کسرهای شصتگانی این دو مقدار تا ثامنه (یعنی رقم «ید»=۱۴)، یکی است. وی سرانجام، این مقدار را در دستگاه شصتگانی چنین میآورد (میانگین دو عدد بالا):
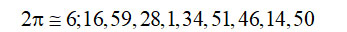
(گ ۲۱؛ نیـز نک : لوکـای، 64-65 , 17-20؛ قربانی، ۱۵۰-۱۵۱؛ هوخندایک، ۷۹).
۷. در اندازۀ خطایی که از رهاکردن کسرهای زاید یا ناقص،
هنگام محاسبات پیشین رخ میدهد (گ ۲۳). در این فصل، کاشانی نشان میدهد که ادامهندادن مراحل محاسبۀ ریشه در فصل ۴، خدشهای به دقت مطلوب او وارد نمیکند؛ یعنی اگر محاسبۀ ریشه با دقت بیشتری نیز انجام میشد، هیچیک از ارقام کسر او تا مرتبۀ ثامنه تغییر نمیکرد (لوکای، 66 ,20-21؛ قربانی، ۱۵۱).
۸. در تبدیل اندازۀ محیط دایره به ارقام هندی (دستگاه شمار دهگانی) با فرض معلومبودن شعاع دایره. در این فصل، کاشانی محیط دایره را، به فرض آنکه شعاع آن واحد باشد، پس درواقع مقدار 2π را در دستگاه شمار دهگانی و با کسرهای اعشاری چنین آورده است:
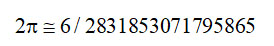
او همچنین دو شعر فارسی و عربی برای حفظ ارقام این عدد سروده است (گ ۲۴؛ نیز نک : لوکـای، 67 ,21-22؛ قربـانی، ۱۵۱- ۱۵۲).
۹. در چگونگی اعمال با دو جدول: این بخش درواقع نوعی آموزش مقدماتی روش استفاده از عدد بهدستآمده برای 2π در محاسبۀ محیط از روی شعاع، و شعاع از روی قطر در هر دو دستگاه دهگانی و شصتگانی، همراه با دو مثال است (گ ۲۴ ب-۲۶ آ؛ نیز نک : لوکای، 22-26؛ قربانی، ۱۵۲).
۱۰. در شناختن تفاوت میان آنچه برای نسبت محیط به قطر دایره در میان ریاضیدانان رواج دارد و آنچه ما به دست آوردهایم. در این فصل، کاشانی مقداری را که برای 2π به دست آورده، با مقادیر بهدستآمده توسط پیشینیان مقایسه کرده، و نشان داده است که مقدار خطا در محاسبۀ دایرهای که شعاعش ۶۰۰‘ ۳ ذراع، و دایرهای دیگر که شعاعش بیش از ۰۰۰‘ ۷ برابر شعاع زمین باشد، تا چه اندازه خواهد بود (گ ۲۶ ب -۲۷ آ؛ نیز نک : لوکای، 26-27, 67-68؛ قربـانی، همانجا؛ نیـز بـرای خلاصهای از کل رسـاله، نک : آذریان، «الرسالة [۴]... »، سراسر مقاله).
در اثبات اشتباه ابوالوفای بوزجانی و ابوریحان بیرونی، که در آن برای اشتباهاتی که به آن دو نسبت داده، دلیل آورده است (گ ۲۷ آ - ۲۹ آ؛ نیز نک : لوکای، 21-22؛ قربانی، ۱۵۲-۱۵۳).
از رسالۀ محیطیه چند دستنویس در دست است که دستنویس شمارۀ ۷۵۶ موزۀ نظامی استانبول مبنای کار پاول لوکای بوده است (نک : دنبالۀ مقاله)؛ اما وی به ارزشمندترین این دستنویسها، یعنی دستنویس شمارۀ ۳۸۹‘۵ کتابخانۀ آستان قدس رضوی به خط خود کاشانی، دسترسی نداشته است. این دستنویس زمانی در اختیار ملک محمد اصفهانی، فقیه و ریاضیدان ایرانی و نویسندۀ رسالاتی در ریاضیات و مباحث فقهی (در ۹۷۱-۹۸۴ ق)، بوده، و سپس به دست دانشمند پرآوازه، شیخ بهایی، رسیده است (برای ویژگیهای نسخه و یادداشتهای ملک محمد و شیخ بهایی، نک : کرامتی، مقدمه بر ... ، ۲۹-۳۲).
یان پیتر هوخندایک در مقدمۀ انگلیسی چاپ نسخهبرگردان سیاه و سفید این دستنویس (نک : ص 86-87)، با اشاره به ۳ مورد که به گمان وی در دستنویس آستان قدس اشتباه، و در دستنویس استانبول درست آمده، بر آن است که این انجامه را نمیتوان سندی معتبر بر کتابت این دستنویس توسط خود کاشانی دانست؛ اما یونس کرامتی (همان، ۳۲-۳۳) نشان داده است که هر ۳ موردْ اشتباهِ خوانشِ هوخندایک بوده، و ضبط دستنویس آستان قدس درست است.
تردید هوخندایک، حتى اگر پذیرفتنی باشد، قدمت نسخه را زیر سؤال نمیبرد، زیرا بیگمان نسخه هنگام رسیدن به دست شیخ بهایی، چندان قدمت داشته است که آن را دستنویس خود مؤلف و کتابتشده در ۸۲۷ ق بداند. با توجه به این نکته و نیز قدمت خط رساله، میتوان کتابت آن را در سدۀ ۹ ق/ ۱۵ م، و چهبسا نیمۀ نخست این سده (نزدیک به روزگار مؤلف) مسلم دانست. از این گذشته، مقایسۀ نمونههایی از خط کاشانی با رسالۀ محیطیه نیز بر کتابت این دستنویس توسط خود کاشانی دلالت دارد (همان، ۳۳-۳۵).
متن کامل رسالۀ محیطیه تاکنون چاپ نشده است. متن عربی بخش آغازین و پایانی این اثر به همراه ترجمه و شرح آلمانی پاول لوکای، پس از مرگ او در ۱۹۵۳ م منتشر شد. سپس ابوالقاسم قربانی در کاشانینامه خلاصهای فارسی از این اثر را همراه با شرح روش کاشانی منتشر کرد.
هوخندایک در ضمن مقالهای دربارۀ رسالۀ محیطیه، در کنار انتشار نسخهبرگردانی سیاه و سفید از آن، شرحی نیز دربارۀ این رساله نوشت و با مراجعه به متن دستنویس حاضر، برخی اشکالات متن عربی و ترجمۀ لوکای را نیز برطرف ساخت. بنابه گزارش وی، نخستین کسی که توانست به تقریبی دقیقتر از تقریب کاشانی دست یابد، لودولف ون کولن هلندی بود که ۱۷۲ سال پس از نگارش رسالۀ محیطیه کتابی دراینباره منتشر کرد.
محمد ک. آذریان در ۲۰۰۴ م، مقالهای دربارۀ قضیۀ مطرحشده در فصل نخست رساله نوشت؛ سپس در ۲۰۰۹ م مقدمۀ این رساله را با استفاده از ترجمۀ فارسی قربانی، به انگلیسی ترجمه کرد و سال بعد نیز شرحی مختصر دربارۀ این رساله به انگلیسی نوشت (نک : مآخذ مقاله).
تاریخنگاران ریاضیات، پیش از آشنایی با آثار کاشانی، بر آن بودند که سیمون استوین، دانشمند هلندیزبان بلژیکی، نخستین کسی بوده است که اهمیت کسرهای دهدهی را دریافته، چگونگی کار با آنها را بهطور کامل شرح داده، و بهکارگیری آنها را به دیگران توصیه کرده است.
در سال ۱۹۲۳ م، دیوید یوجین اسمیث بـا اشاره به اینکه روش یـافتن ریشه بـا افزودن صفرهـا (جذر بالاصفـار؛ دراینبـاره، نک : کرامتی، «تاریخ ... »، ۲۹۹-۳۰۰) روشی بسیار کهن بوده است و هندیها، مسلمانان و دستکم پدیدآورندۀ یکی از روایتهای لاتینی حساب خوارزمی (با عنوان «درآمد خوارزمی بر حساب کاربردی[۵]» که در تاریخ ریاضیات به LA مشهور است، دراینباره، نک : همان، ۳۰۲-۳۰۳) با آن آشنا بودهاند، تأکید کرد که این ریاضیدانان بیگمان کسرهای اعشاری را میشناختهاند؛ زیرا پاسخی که از این راه به دست میآید، همیشه بخش اعشاری دارد. از جملۀ موارد دیگری که کسرهای اعشاری بهصورت ضمنی در آن مطرح شدهاند، جدولهایی برای ریشۀ دوم اعداد است که در آنها اعداد در ۰۰۰‘۱۰۰ ضرب شده بودند، مانند جدولی که آدام ریسه در ۱۵۲۲ م در کتاب خود، «محاسبۀ خطها و منحنیها»، تنظیم کرده بود. شماری از شمارگران نیز هنگام تنظیم جدولنگاشتهای مثلثاتی، شعاع دایرۀ مثلثاتی را بهجای «۶۰» (روش کهن) یا «۱» (مانند امروز) برابر با ۰۰۰‘۰۰۰‘۱ یا ۰۰۰‘۱۰۰ در نظر میگرفتند که در این صورت نیز اعداد جدول عملاً کسرهایی اعشاری بودند (اسمیث، II/ 236-238).
اسمیث افتخار برداشتن گامهای نخست در کشف کسرهای دهدهی را بهصراحت از آن کاشانی میدانست، زیرا به گمان او، ریاضیدانان پیش از کاشانی این بخش اعشاری را بهصورت کسری که مخرج آن توانی از ۱۰ باشد نمینوشتند، بلکه آن را مستقیماً به کسرهای شصتگانی یا کسرهای هندی رایج تبدیل میکردند؛ درحالیکه کاشانی قوانین مربوط به این کسرها را میشناخت و در رسالۀ محیطیه نیز نهتنها نسبت محیط به شعاع دایره (2π) را بهصورت کسری اعشاری نشان داده، بلکه برای آشنایی بیشتر خواننده نمونههایی از کار با این کسرها را (در فصل هشتم و نهم) ارائه کرده بود (II/ 239-240). بااینهمه، اسمیث بر آن بود که کریستُف رودولف (۱۴۹۹-۱۵۴۵ م) نخستین ریاضیدانی است که شایستگی عنوان مخترع کسرهای اعشاری را دارد؛ زیرا وی در کتاب خود، که در ۱۵۳۰ م منتشر شد[۶]، در ضمن یک مثال، نهتنها نشان میدهد که بهخوبی کار با این نوع کسرها را میداند، بلکه برای ثبت آنها نشانۀ «|» را دقیقاً مانند ممیز امروزی («/ » در فارسی و «.» در زبانهای اروپایی) به کار میبرد (برای مثال، 413. 4375=413|4375؛ البته این ابتکاری است که خواهیم گفت مدتها پیش از وی، در کتاب اقلیدسی آمده بود). اما به نظر میرسد که کتاب رودولف مورد توجه واقع نشد، یا به گفتۀ اسمیث (II/ 236-238)، این کتاب چنانکه بایدوشاید فهمیده نشد.
در سال ۱۵۸۵ م، سیمون استوین جزوۀ کوچکی با عنوان «اعشار[۷]» به زبان فلاندری منتشر کرد که نخستین اثر مستقل دربارۀ کسرهای اعشاری به شمار میرود. او در همان سال نیز ترجمۀ فرانسوی [۸]آن را در ضمن جلد دوم «کتاب حساب[۹]» که عنوان مستقل «کاربرد حساب[۱۰]» را بر خود داشت، منتشر کرد (برای بحثی مفصل دربارۀ این اثر و نسخهبرگردان روایت فرانسوی آن، نک : سارتن، 153-244). این کتاب خیلی زود جای خود را در میان ریاضیدانان آن روزگار باز کرد و رابرت نورتون آن را به انگلیسی برگرداند که در ۱۶۰۸ م در لندن به چاپ رسید[۱۱].
جالب آنکه استوین برای نمایش و خواندن کسرهای اعشاری روشی بسیار ابتدایی به کار میبرد. بهطور مثال، وی عدد 37.875 را بهصورت 37⓪8①7②5③ مینوشت و آن را «۳۷ صحیح، ۸ اولى (دقیقه)، ۷ ثانیه و ۵ ثالثه[۱۲]» میخواند (همو، 163؛ اسمیث، II/ 242-243) و از این لحاظ، هم از پیشینیان مسلمان خود و هم از رودولف عقبتر بود.
پس از انتشار پژوهشهای پاول لوکای دربارۀ رسالۀ محیطیه و مفتاح الحساب، بر همگان مسجل شد که کاشانی نهتنها در ۸۲۷ ق/ ۱۴۲۳ م، یعنی دستکم ۱۵۰ سال پیش از اروپاییان، این کسرها را به قیاس کسرهای شصتگانی اختراع کرده، و در رسالۀ محیطیه به کار برده، و چند مثال از چگونگی کار با این کسرها را آورده، بلکه در ۸۳۰ ق و در مفتاح الحساب بهتفصیل دربارۀ آنها سخن گفته، و بهکارگیری آنها را به دیگران توصیه کرده است.
نزدیک به دو دهۀ بعد، احمد سلیم سعیدان با انتشار متن عربی الفصول فی الحساب الهندی نوشتۀ احمد بن ابراهیم اقلیدسی، نشان داد که وی در ۳۴۱ ق این کسرها را میشناخته، و برای متمایزکردن بخش کسری و صحیح اعداد، نشانهای روی مرتبۀ یکان آنها میگذاشته، که درواقع همان روشی است که ما امروزه به کار میبریم، با این تفاوت که این نشانه را میان یکان و دهم اعشار میگذاریم.
برای نمونه، اقلیدسی در بحث تقسیم متوالی بر ۲، این اصل را که «نصف ”یکی“ در هر مرتبهای برابر است با ۵ در مرتبۀ پایینتر»، بهمراتب کمتر از یکان تعمیم میدهد و میافزاید که روی مرتبۀ یکان عدد نشانهای میگذاریم [تا مرتبۀ ارقام اشتباه نشود]. او برای نمونه، عدد «۱۹» را بر ۲۵تقسیم، و نتایج تقسیمات پیاپی را بهترتیب ۵´۹، ۷۵´۴، ۳۷۵´۲، ۱۸۷۵´۱ و سرانجام، ۵۹۳۷۵´۰ ثبت، و دربارۀ عدد ۳۷۵´۲ تأکید میکند که اگر بخواهیم این عدد را بخوانیم، باید بگوییم «۲ و ۳۷۵ [جزء] از هزار»، و در مورد ۵۹۳۷۵´۰ نیز میگوید که این عدد ۵۹۳۷۵ [جزء] از صدهزار است. البته به نظر میرسد که این کسرها برای اقلیدسی اهمیت ویژهای نداشته است و به همین دلیل تنها یک بار نتیجۀ محاسبه را به همان صورت اعشاری رها میکند؛ اما در دیگر موارد، این کسرها را به معادل هندی آنها تبدیل میکند (ازجمله در نمونۀ یادشده: «نصف و نصف یکهشتم و ربع یکهشتم»، نک : ص ۱۳۴، ۱۴۵-۱۴۶، ۱۵۰- ۱۵۱، ۲۵۴-۲۵۵؛ سعیدان، ۴۴۹، ۴۸۰-۴۸۱؛ قربانی، ۱۳۴-۱۳۶).
گویا ریاضیدانان دورۀ اسلامی الفصول اقلیدسی را، بهرغم اهمیت ذاتی آن، نمیشناختهاند یا اهمیت آن را درنیافته، و بدان بیتوجه بودهاند؛ زیرا دستکم تاکنون هیچ نشانهای از تأثیر محتویات این کتاب بر آثار ریاضیدانان بعدی یافت نشده است.
سرانجام، در سال ۱۹۷۸ م/ ۱۳۵۷ ش؛ رشدی راشد در مقالهای مفصل نشان داد که سموأل بن یحیى مغربی، ریاضیدان نامدار پیرو مکتب کرجی، در ۵۶۸ ق/ ۱۱۷۳ م، یعنی حدود ۱۶۰ سال پیش از کاشانی، در القوامی فی الحساب الهندی این کسرها را مستقل از اقلیدسی به کار برده، و بر اهمیت بسیار آنها نیز تأکید کرده است. بااینهمه، راشد به این نکتۀ ظریف اشاره میکند که این کسرها در القوامی سموأل نیز نام خاصی ندارند و این کاشانی است که آنها را «کسرهای اعشاری» مینامد و با این نامگذاری، هویتی کاملاً مستقل برای آنها قائل میشود. در هر صورت، به نظر میرسد که رواج کاربرد این کسرها در میان ریاضیدانان دورۀ اسلامی مدیون کاشانی بـاشد؛ زیرا تاجاییکه میدانیم، القوامی سموأل نیز همچون الفصول اقلیدسی در میان ریاضیدانان بعدی ناشناخته، یا دستکم تأثیر آن بسیار اندک بوده است.
سموأل، که همچون کرجی در حساب چندجملهایها بسیار زبردست بود، گویا با مقایسۀ «مرتبۀ اعداد در دستگاه شمار دهگانی» و «توان مجهول در چندجملهایها»، کسرهای دهدهی را به قیاس آنچه ما امروزه توانهای منفی مجهول مینامیم، اختراع، و به عبارت دیگر، این دو رشته را با یکدیگر مقایسه کرده است:
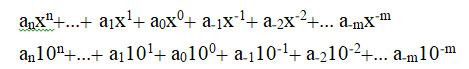
که دومی عددی است که میتوان آن را چنین نشان داد:
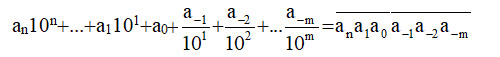
که در آن ana1a0 و a-1a-2a-m ارقام بخشهای صحیح و اعشاری عدد هستند (سموأل، جم ؛ نیز نک : راشد[۱۳]، جم ). اما کاشانی که گویا از کار سموأل خبر نداشته، تأکید داشته که این کسرها را به قیاس کسرهای شصتگانی اختراع کرده است.
اقلیدسی، احمد بن ابراهیم، الفصول فی الحساب الهندی، به کوشش احمد سلیم سعیدان، عمان، ۱۹۸۴ م؛ سعیدان، احمد سلیم، مقدمه و شرح الفصول فی حساب الهنـدی (نک : هم ، اقلیدسی)؛ سموأل بن یحیى مغربی، القوامی فی الحساب الهندی (نک : مل ، راشد)؛ غیاثالدین جمشید کاشانی، الرسالة المحیطیة، چ تصویری، به کوشش یونس کرامتی، تهران، ۱۳۹۲ ش؛ قربانی، ابوالقاسم، کاشانینامه (احوال و آثار غیاثالدین جمشید کاشانی)، تهران، ۱۳۶۸ ش؛ کرامتی، یونس، «تاریخ تحول حساب در ایران»، تاریخ جامع ایران، تهران، ۱۳۹۳ ش؛ ج ۱۳؛ همو، مقدمه بر الرسالة المحیطیة (نک : هم ، غیاثالدین جمشید کاشانی)؛ نیز:
Azarian, M. K., «The Introduction of Al-Risāla al-Muhītīyya: An English Translation», International Journal of Pure and Applied Mathematics, 2009, vol. LVII, no. 2; id., «Al-Kāshī’s Fundamental Theorem», ibid., 2004, vol. XIV, no. 4; id., «Al-Risāla al-Muhītīyya: A Summary», Missouri Journal of Mathematical Sciences, 2010, vol. XXII, no. 2; Hogendijk, J. P., «Al-Kāshī’s Determination of π to 16 Decimals in an Old Manuscript», Zeitschrift für Geschichte der arabisch-islamischen Wissenschaften, 2002-2003, vol. XVIII; Luckey, P., Der Lehrbrief über den Kreisumfang, Berlin, 1953; Rashed, R., «L’Extraction de la Racine nième et l’Invention des Fractions Décimales (XIe-XIIe Siècles)», Archive for History of Exact Sciences, 1978, vol. XVIII, no. 3; Sarton, G., «The First Explanation of Decimal Fractions and Measures (1585) Together With a History of the Decimal Idea and a Facsimile (no. XVII) of Stevin’s Disme», Isis, 1935, vol. XXIII, no. 1; Smith, D. E., History of Mathematics, New York, 1925.
ازم به ذکر است، ماجراجویی برای دستیابی برای تقریبهای دقیقتر برای این عدد مرموز، همچنان ادامه دارد و در سالهای اخیر توفیقاتی نیز در این خصوص حاصل شده است. با شروع قرن بیستم، حدود ۵۰۰ رقم پی محاسبه شده بود. با پیشرفت تکنولوژی و بهلطف محاسبات کامپیوتری، اکنون ما تا دهها تریلیون رقم اول این عدد را میدانیم. در سال ۲۰۱۹، اِما هاروکا، مشاور توسعه فضای ابری در گوگل، موفق شد با استفاده از ۱۷۰ ترابایت داده و برنامه چندرشتهای موسوم به y-cruncher، دقیقترین مقدار عدد پی در جهان را تا آن زمان محاسبه کند که شامل ۳۱٫۴ تریلیون رقم اعشار میشد. محاسبه این ارقام ۱۲۱ روز طول کشید. ناگفته نماند سال ۲۰۲۰ رکورد محاسبه بیشترین ارقام پی به ۵۰ تریلیون رسید. آخرین دستاورد در این حوزه، مربوط به محققان دانشگاه علوم کاربردی گروبندن (Graubuenden) سوئیس است که با استفاده از یک ابررایانه موفق به محاسبه عدد "پی" تا ۶۲.۸ تریلیون رقم شدند. به گفتهی مرکز تجزیه و تحلیل دادههای این دانشگاه، محاسبه این عدد ۱۰۸ روز و ۹ ساعت به طول انجامیدو دستیابی به آن دوبرابر سریعتر از رکورد کارمند گوگل در سال ۲۰۱۹ و سه و نیم برابر سریعتر از آخرین رکورد ثبت شده در سال ۲۰۲۰ بود.
عدد پی تا ۱۰۵ تریلیون رقم بدست آمد و رکورد جهانی را شکست!
در روز Pi (14 مارس)، «Solidigm» یک شرکت ذخیرهسازی رایانه در ایالات متحده مستقر در کالیفرنیا، در بیانیهای اعلام کرد که پی را تا حدود 105 تریلیون رقم اعشار محاسبه کرده است. برای بیان این موضوع، اگر این عدد را روی کاغذ با استفاده از فونت 10 نقطهای در یک خط پیوسته تایپ کنید، طول آن حدود 3.7 میلیارد کیلومتر خواهد بود، به این معنی که میتواند از زمین تا جایی بین اورانوس و نپتون برسد و جالب است بدانید رقم 105 تریلیون عدد پی، عدد 6 است.
این محاسبه که حدود 75 روز طول کشید و با 36 درایو حالت جامد (SSD) اختصاصی این شرکت، یک رسانه ذخیرهسازی که در بسیاری از جدیدترین لپتاپها نصب شده است، انجام شد که در مجموع حدود 1 پتابایت (1 میلیون گیگابایت) داده مصرف کرد. همچنین برای انجام بخشی از محاسبات به پردازندهها با اجزای قدرتمندتر نیاز است برای این که زمان انجام محاسبات لازم را کاهش میدهند. با این حال، ذخیره سازی قابل اعتماد و با ظرفیت بالا مسلماً مهمتر است زیرا شما نیاز به ذخیره حجم عظیمی از دادهها در چنین فرآیندی دارید.
به گفته برایان بیلر، مالک Solidigm، این دستاورد، دستاورد کوچکی نبود چرا که نیاز به برنامهریزی دقیق، بهینه سازی و اجرا داشت. در آوریل 2023، Solidigm به 100 تریلیون رقم پی دست پیدا کرد که این مقدار توسط Google Cloud در سال 2022 محاسبه شده بود. قبل از آن، رکورد 62.8 تریلیون رقم بود که طی 108 روز توسط یک ابررایانه در دانشگاه علوم کاربردی گریسونز در سوئیس در سال 2021 محاسبه شد. حتی، رکورد 50 تریلیون رقمی در سال 2020 توسط تیموتی مولیکان از هانتسویل، آلاباما، با استفاده از رایانه شخصی ثبت شد.
با استفاده از کامپیوتر مغز انسان، برای بیشترین رقم پی حفظ شده توسط یک فرد، رکورد جهانی در حال حاضر 70000 است که توسط راجویر مینا در دانشگاه VIT هند در 21 مارس 2015 بر اساس رکوردهای جهانی گینس به دست آمد. همانطور که کامپیوترها در آینده قدرتمندتر میشوند، ما به ناچار شروع به کشف تکههای بزرگتر و بزرگتر پی خواهیم کرد. با این حال، مهم نیست که کامپیوترها چقدر قدرتمند شوند، به دلیل ماهیت نامتناهی آن، هرگز نمیتوانیم کل عدد را کشف کنیم.
منبع: livescience