 که در آن
که در آن  و
و  اعداد ثابتی میباشند
اعداد ثابتی میباشند  مخالف صفر) و
مخالف صفر) و  هم مجهول میباشد. پاسخ چنین معادله ای برابر است با منفی
هم مجهول میباشد. پاسخ چنین معادله ای برابر است با منفی  تقسیم بر
تقسیم بر  .
.بسم الله الرحمن الرحیم
فهرست جبرمعادلهٔ خطی
(به انگلیسی: Linear equation) یک معادلهٔ جبری است که در آن هر جمله، یا متغیر است یا حاصلضرب یک ثابت و تنها یک متغیر با توان یک. این معادلات ممکن است یک یا چند متغیر داشته باشند. این معادلات دارای یک ریشه بوده و در صورتی که همهٔ اعداد و ضرایب معادله حقیقی باشند آنگاه جواب نیز در مجموعه اعداد حقیقی تعیین خواهد شد. شکل عموم این نوع معادلات بدین صورت است: 






دستگاه معادلات خطی
در ریاضیات، دستگاه معادلات خطی به معنی مجموعهای از تعدادی معادلهٔ خطی است.[۱] برای مثال:
یک دستگاه از ۳ معادلهٔ خطی با ۳ مجهول 
جواب یک دستگاه خطی به معنی مقداردهی به هر مجهول است به طوری که با جایگذاری آنها معادلات دستگاه برقرار باشند. جواب مثال مذکور x = 0 , y = 1 , z = 0 است. جواب یک دستگاه ممکن است یکتا نباشد یا ممکن است جوابی وجود نداشته باشد.
این مفهوم پایه و اساس جبر خطی است و نقش مهمی در مهندسی، فیزیک، شیمی، علوم کامپیوتر و اقتصاد دارد. الگوریتمهای پیدا کردن جواب این دستگاهها بخش مهمی از جبر خطی عددی است. برای سادگی حل سامانههای پیچیده، میتوان دستگاهی از معادلات غیرخطی را با خطیسازی به یک دستگاه معادلهٔ خطی تقریب زد
سایت ویکی پدیا
سایت ریاضیکا
در درسنامهٔ معادلات خطی ریاضی نهم قصد داریم دستگاههای معادلات خطی را معرفی کرده و روش حل آنها را بررسی کنیم. به طور کلی معادلات خطی از ضرایب ثابت و یا متغیرهایی با درجهٔ یک تشکیل شدهاند. برای یادآوری بیشتر میتوانید درسنامهٔ معادله خط ریاضی نهم را مرور کنید. اما دستگاه معادلات خطی چیست؟ در این درسنامه قصد داریم تا به همین سوال پاسخ دهیم. با ما تا انتها همراه باشید.
اگر به جای یک معادلهٔ خطی، چند معادلهٔ خطی با متغیرهای مشترک داشته باشیم، دستگاه معادلات خطی داریم. به اعدادی که در صورت جاگذاری در متغیرها در معادله صدق کنند، جواب دستگاه معادلات میگوییم. بگذارید مثال بزنیم. معادلهٔ y=x+2 خطی است. اگر به جای x مقدار 1 و به جای y مقدار 2 را قرار دهیم، رابطهٔ y=x+2 برقرار است. بنابراین به x=1 و y=3 یک جواب برای معادلهٔ y=x+2 میگوییم. معادلهٔ y=x+2، دسته جوابهای دیگری نیز دارد. مثلاً x=2 و y=4 نیز در معادله صدق میکنند. حال فرض کنید به جای یک معادله، دو معادله داشتیم و به دنبال xها و yهایی بودیم که به طور همزمان در هر دو معادله صدق کنند. مثلاً فرض کنید دو معادلهٔ y=2x+1 و y=x+3 را داریم و به دنبال دسته جواب هایی هستیم که در هر دو صدق کنند. در این صورت به {y=2x+1y=x+3 دستگاه معادله خطی میگوییم. اگر مقدار x را برابر با 2 و مقدار y را برابر با 5 قرار دهیم، x و y در هر دو معادله صدق میکنند. در ادامهٔ درسنامه روش حل دستگاههای معادلات خطی را بررسی خواهیم کرد.
روش حل دستگاه معادلات خطی
از آنجاییکه در کتاب درسی، دستگاههایی که دو معادله و دو متغیر دارند، بررسی میشوند، ما نیز به بررسی این دستگاهها میپردازیم. البته روش حل دستگاههای دیگر نیز به همین صورت است. به طور کلی، برای حل دستگاههای معادلات خطی که دارای دو معادله و دو مجهول هستند، باید یک مجهول را به طریقی حذف کرده تا یک معادلهٔ یک مجهولی داشته باشیم. برای این کار، سه روش متداول وجود دارد:
در قسمتهای بعدی از درسنامهٔ دستگاه معادلات خطی نهم ، هر یک از این سه روش را بررسی میکنیم.
...
برای حل دستگاه معادلات خطی میتوان معادلات را با یکدیگر جمع کرده تا یکی از متغیرها حذف شود و دستگاه تبدیل به یک معادلهٔ یک مجهولی گردد. به این روش، روش حذفی میگوییم. اما منظور از جمع معادلات و حذف متغیر چیست؟ فرض کنید میخواهیم دستگاه {x+y=2x−y=4 را حل کنیم. در این صورت، طرفهای چپ دو معادله را با هم و طرفهای راست را با هم جمع کرده و با یکدیگر برابر قرار میدهیم. برای اینکه بهتر متوجه شوید به تصویر پایین دقت کنید:
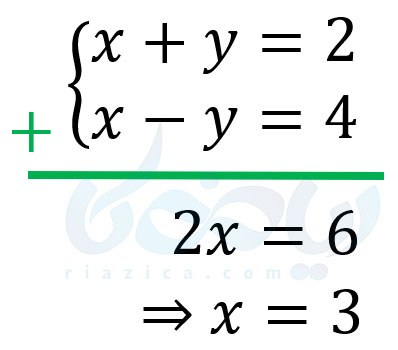
همان طور که دیدید، با انجام این کار، دستگاه به معادلهٔ یک مجهولی 2x=6 تبدیل میشود. پاسخ این معادلهٔ یک مجهولی نیز، x=3 است. حال کافی است به دستگاه اولیه برگردیم و مقدار x را در یکی از معادلات، برابر با 3 قرار دهیم. مثلاً، کافی است در معادلهٔ x+y=2 که در دستگاه، قبل از جمع معادلات وجود داشت، مقدار x را برابر با 3 قرار دهیم. در این صورت داریم:
3+y=2
⇒y=−1
در نتیجه، [3−1] جواب دستگاه معادلات خطی است. باید توجه داشت که گاهی لازم است ابتدا یکی از معادلات را در یک عدد مناسب ضرب کرده و سپس با معادلهٔ دوم جمع کنیم. برای پیدا کردن عدد مناسب، ابتدا ببینید چه متغیری را میخواهید حذف کنید. مثلاً فرض کنید میخواهیم متغیر x را در دو معادله حذف کنیم. باید یکی از معادلات را در عددی ضرب کنیم به طوری که ضریب x در دو معادله قرینهٔ یکدیگر شود. در انتها دو معادله را با یکدیگر جمع میکنیم تا متغیری که مد نظرمان بود حذف گردد. برای اینکه بهتر متوجه شوید، به مثالهای بعدی از درسنامهٔ دستگاه معادلات خطی نهم توجه کنید.
مثال 4:دستگاه معادلات خطی {2x−5y=24x+3y=17 را حل کنید.
حل: سعی می کنیم متغیر x را از دو معادله حذف کنیم. ضریب متغیر x در معادلهٔ اول برابر با 2 و در معادلهٔ دوم برابر با 4 است. بنابراین، کافی است معادلهٔ اول را در عدد −2 ضرب کنیم تا ضریب x در دو معادله، قرینهٔ یکدیگر شود. به این ترتیب داریم:
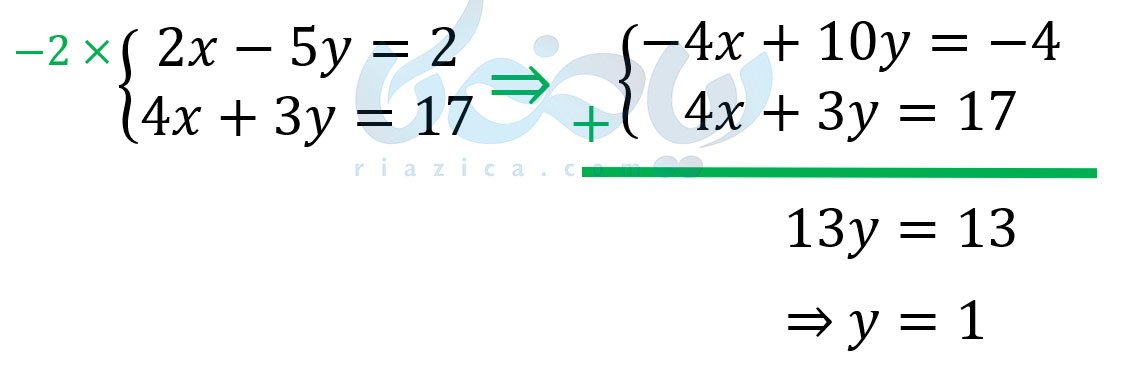
حال باید y را در یکی از معادلات دستگاه برابر با 1 قرار داده تا x را به دست آوریم. معادلهٔ 2x−5y=2 را برای این کار انتخاب میکنیم. بنابراین داریم:
2x−5=2
⇒2x=7
⇒x=72
در نتیجه، y=1 و x=72 جواب دستگاه معادلات خطی ماست.
مثال 5: جوابهای دستگاه معادلات خطی {x3+y2=3−2x9+y6=−1 را بیابید.
حل: این بار سعی میکنیم متغیر y را حذف کنیم. ضریب متغیر y در معادلهٔ اول برابر با 12 و در معادلهٔ دوم برابر با 16 است. بنابراین، کافی است معادلهٔ دوم را در عدد −3 ضرب کنیم تا ضریب y در دو معادله، قرینهٔ یکدیگر شود. به این ترتیب داریم:
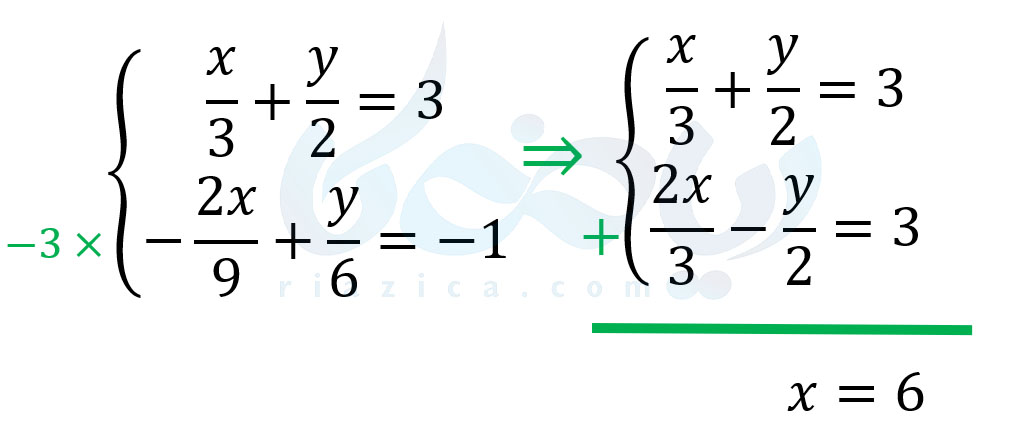
بنابراین x=6 است. حال باید مقدار x را در یکی از معادلات دستگاه برابر با 6 قرار داده و y را به دست آوریم. معادلهٔ x3+y2=3 را برای این کار انتخاب میکنیم. بنابراین داریم:
2+y2=3
⇒y2=3−2=1
⇒y=2
سایت خوش آموز
با وجود اینکه حل کردن دستگاه معادلات خطی با روش ترسیم نمودار، سرشار از سرگرمی می باشد، روش ترسیم نمودار یک اشکال بزرگ دارد: پیدا کردن پاسخهایی که اعداد صحیح نمی باشند، تقریباً غیرممکن است. همچنین روش ترسیم نمودار زمان بر است و نیاز به دقت فراوان دارد. روش هایی که ریاضیدانان برای حل کردن دستگاه های معادلات خطی ترجیح می دهند، شامل استفاده از جبر می باشد. دو روش بیشتر ترجیح داده شده و رایج، برای حل کردن دستگاه معادلات خطی شامل روش حذف (elimination) و روش جایگذاری (Substitution) می باشند. در این آموزش به روش حذف می پردازیم و سایر روشها را نیز در ادامۀ همین فصل بررسی می کنیم. تشخیص اینکه باید از کدام روش استفاده کنید، بستگی به شکل آغازین معادلات و البته ترجیح شخصی شما دارد.
یادتان باشد: روش حذف (elimination)، همچنین با اسامی ترکیب خطی (linear combination) و جمع/تفریق (add/subtract) نیز شناسایی می شود. کلمۀ حذف، کاری را که دقیقاً در این روش انجام می شود، توصیف می کند، اما کلمۀ جمع/تفریق چگونگی انجام این کار را بازگو می کند.
برای پیش بُردن روش حذف، شما نیاز دارید تا آن دو معادله را با یکدیگر جمع بزنید، یا یکی از آنها را از دیگری تفریق کنید، و یکی از متغیرها را حذف کنید تا از شر آن خلاص گردید. گاهی اوقات شما مجبور می شوید قبل از اینکه عملیات جمع یا تفریق معادله ها را انجام بدهید، یک یا هر دو معادله را بر عددی که با دقت انتخاب شده است ضرب کنید.
به عنوان مثال، دستگاه معادلات زیر را در نظر بگیرید:
در این دستگاه معادلات، شما می توانید با جمع کردن دو معادله با یکدیگر متغیر y را حذف کنید. دو جملۀ y در این دو معادله، معکوس یکدیگر می باشند. عبارت حاصل از جمع زدن این دو معادله برابر با 5x=20 می باشد. با تقسیم کردن هر سمت از این معادله بر 5 ، به x=4 می رسید. هنگامیکه x=4 را در معادلۀ اول قرار می دهید، به 3(4)−5y=2 می رسید. با حل کردن این معادله برای y به y=2 می رسید. بنابراین، پاسخ این دستگاه x=4,y=2 می باشد. اگر نمودار این دو خط متناظر با این دو معادله را ترسیم کنید، خواهید دید که آنها در نقطۀ (4,2) یکدیگر را قطع می کنند.
دستگاه معادلات زیر را در نظر بگیرید:
در این دستگاه معادلات قبل از آنکه دو معادله را با هم جمع یا تفریق کنید، نیاز به اندکی تنظیمات دارید. اگر این دو معادله را در شکل فعلی شان با یکدیگر جمع بزنید، به معادله دیگری می رسید: 5x−7y=43 . شما یک معادلۀ کاملاً زیبا را ساخته اید، و پاسخ آن نیز با دو معادلۀ قبل یکسان می باشد، اما این معادلۀ سوم در پیدا کردن پاسخ دستگاه، کمکی به شما نمی کند. قبل از اینکه جمع یا تفریق کنید، نیاز دارید تا مطمئن شوید یکی از این متغیرها در این دو معادله، باید با همتایش در معادلۀ دیگر یکسان یا متضاد آن باشد؛ در این صورت، وقتیکه معادلات را جمع یا تفریق می کنید، آن متغیر حذف خواهد شد.
شما چندین گزینۀ مختلف برای انتخاب دارید تا معادلات موجود در این مثال را برای حذف کردن متغیرها آماده سازید:
اگر در مثال قبلی انتخاب شما این باشد که با ضرب کردن معادلۀ اول در 2 و معادلۀ دوم در −3 قصد حل کردن دستگاه را دارید، نسخۀ جدیدی از دستگاه را به شرح زیر بدست خواهید آورد:
با جمع کردن این دو معادله با یکدیگر، به 11y=−44 می رسید، متغیرهای x حذف می شوند. با تقسیم کردن هر سمت از این معادلۀ جدید بر 11 ، به y=−4 می رسید. این مقدار را در معادلۀ اصلی اول جایگزین کنید.
با جایگزینی −4 به جای متغیر y ، به 3x−2(−4)=17 می رسید. با حل کردن آن برای x به x=3 می رسید. اکنون با قرار دادن 3 و −4 در معادلۀ اصلی دوم، پاسخهای بدست آمده را درست آزمایی کنید. با جایگزینی این مقادیر به نتایج زیر می رسید:
درست آزمایی با موفقیت انجام شد! پاسخ این دستگاه (3,−4) می باشد.
هنگامی که نمودار دستگاه های معادلات خطی را ترسیم می کنید، اگر دستگاهی خطهای موازی تولید کند یا دارای معادلاتی باشد که خط یکسانی را ارائه کنند، تشخیص این موارد از روی نمودار، تقریباً واضح می باشد. با این وجود، از لحاظ جبری شما نیازی ندارید تا برای تشخیص این وضعیت ها نمودار خطها را ترسیم کنید؛ شما صرفاً باید بدانید، دنبال چه چیزی باشید.
به عنوان مثال، هنگامی که دستگاه زیر را حل می کنید، معادلۀ دوم را در −1 ضرب می کنید و سپس معادلات را با یکدیگر جمع می زنید. نتیجۀ بدست آمده 0=5 می باشد. این زیاد خوب نیست. این گزارۀ غلط سیگنالی به شما می دهد که این دستگاه دارای پاسخی نمی باشد و خطها موازی هستند.
در مقابل، هنگامی که دو معادله داشته باشید که هر دوی آنها اشاره به خط یکسانی داشته باشند و آن معادلات را با روش حذف با یکدیگر جمع بزنید، به معادله ای خواهید رسید که همواره صحیح می باشد، مانند 0=0 یا 5=5 .